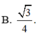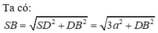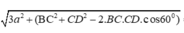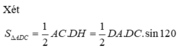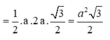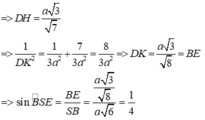Các câu hỏi tương tự
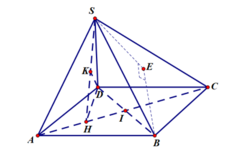
Cho hình chóp S.ABCD có ABCD là hình bình hành, AB2a, BCa,
A
B
C
⏜
120
0
. Cạnh bên
S
D
a
3
và SD vuông góc với mặt phẳng đáy (tham khảo hình vẽ bên). Tính sin của góc tạo bởi SB và mặt phẳng (SAC). A.
3
4
B. ...
Đọc tiếp
Cho hình chóp S.ABCD có ABCD là hình bình hành, AB=2a, BC=a, A B C ⏜ = 120 0 . Cạnh bên S D = a 3 và SD vuông góc với mặt phẳng đáy (tham khảo hình vẽ bên). Tính sin của góc tạo bởi SB và mặt phẳng (SAC).

A. 3 4
B. 3 4
C. 1 4
D. 3 7
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Hai mặt phẳng (SAB) và (SAC) cùng vuông góc với đáy (ABCD) và SA2
α
Tính cosin của góc giữa đường thẳng SB và mặt phẳng (SAD)
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Hai mặt phẳng (SAB) và (SAC) cùng vuông góc với đáy (ABCD) và SA=2 α Tính cosin của góc giữa đường thẳng SB và mặt phẳng (SAD)
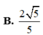
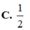
![]()
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA vuông góc với mặt phẳng (ABCD) và SAa
6
. Gọi a là góc giữa đường thẳng SB và mặt phẳng (SAC). Tính sin
α
ta được kết quả là: A.
1
14
B.
2
2
C.
3
2
D. ...
Đọc tiếp
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA vuông góc với mặt phẳng (ABCD) và SA=a 6 . Gọi a là góc giữa đường thẳng SB và mặt phẳng (SAC). Tính sin α ta được kết quả là:
A. 1 14
B. 2 2
C. 3 2
D. 1 5
#SGD Bắc Giang – năm 2017 – 2018~Cho hình chóp S. ABCD có đáy ABCD là hình chữ nhật, ABa, BC a
3
, SAa và SA vuông góc với đáy ABCD. Tính sin α, với α là góc tạo bởi giữa đường thẳng BD và mặt phẳng (SBC).
Đọc tiếp
#SGD Bắc Giang – năm 2017 – 2018~Cho hình chóp S. ABCD có đáy ABCD là hình chữ nhật, AB=a, BC = a 3 , SA=a và SA vuông góc với đáy ABCD. Tính sin α, với α là góc tạo bởi giữa đường thẳng BD và mặt phẳng (SBC).
![]()
![]()
![]()
![]()
Cho hình chóp S. ABCD có đáy ABCD là hình vuông có độ dài đường chéo bằng a
2
và SA vuông góc với mặt phẳng (ABCD). Gọi α là góc giữa hai mặt phẳng (SBD) và (ABCD). Nếu tan α
2
thì góc giữa hai mặt phẳng (SAC) và (SBC) bằng: A. 300 B. 600 C. 450 D. 900
Đọc tiếp
Cho hình chóp S. ABCD có đáy ABCD là hình vuông có độ dài đường chéo bằng a 2 và SA vuông góc với mặt phẳng (ABCD). Gọi α là góc giữa hai mặt phẳng (SBD) và (ABCD). Nếu tan α = 2 thì góc giữa hai mặt phẳng (SAC) và (SBC) bằng:
A. 300
B. 600
C. 450
D. 900
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB a , BC
a
3
, SA a và SA vuông góc với đáy ABCD. Tính sin
α
với
α
là góc tạo bởi giữa đường thẳng BD và mặt phẳng
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB = a , BC = a 3 , SA = a và SA vuông góc với đáy ABCD. Tính sin α với α là góc tạo bởi giữa đường thẳng BD và mặt phẳng
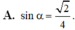
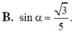
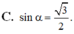
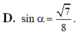
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật,
A
B
a
,
B
C
a
3
,
S
A
a
và SA vuông góc với đáy ABCD. Tính sin
α
với
α
là góc tạo bởi đường thẳng BD và mặt phẳng (SBC)
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, A B = a , B C = a 3 , S A = a và SA vuông góc với đáy ABCD. Tính sin α với α là góc tạo bởi đường thẳng BD và mặt phẳng (SBC)


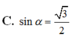

Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA
⊥
(ABCD) và SA a
3
. Gọi
α
là góc tạo bởi giữa đường thẳng SB và mặt phẳng (SAC), khi đó
α
thỏa mãn hệ thức nào sau đây? A. cos
α
2
8
B. sin
α
2
8
C. sin
α
...
Đọc tiếp
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA ⊥ (ABCD) và SA = a 3 . Gọi α là góc tạo bởi giữa đường thẳng SB và mặt phẳng (SAC), khi đó α thỏa mãn hệ thức nào sau đây?
A. cos α = 2 8
B. sin α = 2 8
C. sin α = 2 4
D. cos α = 2 4
Cho hình chóp SABCD có đáy ACBD là hình vuông cạnh
α
, SA vuông góc với mặt phẳng đáy, góc giữa SB và mặt đáy bằng 600. Tính khoảng cách h từ A tới mặt phẳng (SBC)
Đọc tiếp
Cho hình chóp SABCD có đáy ACBD là hình vuông cạnh α , SA vuông góc với mặt phẳng đáy, góc giữa SB và mặt đáy bằng 600. Tính khoảng cách h từ A tới mặt phẳng (SBC)
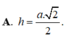
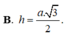
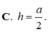
![]()