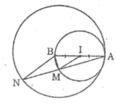
Tam giác AMB nội tiếp trong đường tròn (I) có AB là đường kính nên ![]()
Suy ra: AM ⊥ BM hay BM ⊥ AN
Suy ra: AM = MN (đường kính vuông góc dây cung).

Tam giác AMB nội tiếp trong đường tròn (I) có AB là đường kính nên ![]()
Suy ra: AM ⊥ BM hay BM ⊥ AN
Suy ra: AM = MN (đường kính vuông góc dây cung).
Cho hai đường tròn (O; R) và (O'; r) cắt nhau tại A và B (R > r). Gọi I là trung điểm của OO'. Kẻ đường thẳng vuông góc với IA tại A, đường thẳng này cắt các đường tròn (O; R) và (O'; r) theo thứ tự C và D (khác A).
Gọi K là điểm đối xứng với điểm A qua điểm I. Chứng minh rằng KB vuông góc với AB.
Cho đường tròn (O) và điểm A nằm bên ngoài (O). Kẻ hai tiếp tuyến AM,AN với đường tròn (O) (M,N là các tiếp điểm). Một đường thẳng d đi qua A cắt đường tròn (O) tại hai điểm B và C( AB<AC,d không qua tâm O) . I là trung điểm BC, đường thẳng qua B // AM cắt MN tại E
a) . A, M, O, I, N thuộc ( O )
b) . AB.AC = AM.AM
c) . IE // MC
Cho đường tròn tâm O và đường thẳng d cắt đường tròn tâm O tại hai điểm B và C (d không đi qua O). Trên tia đối của tia BC lấy điểm A (A nằm ngoài đường tròn tâm O). Kẻ AM và AN là các tiếp tuyến với đường tròn tâm O tại M và N. Gọi I là trung điểm của BC, AO cắt MN tại H, và cắt đường tròn tại các điểm P và Q (P nằm giữa A và O), BC cắt MN tại K.
a) Chứng minh 4 điểm O, M, N, I nằm trên cùng một đường tròn và AK. AI=AM2
b) Gọi D là trung điểm HQ, từ H kẻ đường thẳng vuông góc với MD, cắt đường thẳng MP tại E. Chứng minh P là trung điểm của ME.
GIÚP MK VỚI QAQ
Cho đường tròn ( O; R ) và điểm A cố định ngoài đường tròn. Qua A kẻ 2 tiếp tuyến AM, AN với đường tròn (M và N là các tiếp điểm). Một đường thẳng d đi qua A cắt (O;R) tại B và C (AB<AC). Gọi I là trung điểm BC
a, Chứng minh A, M, N, O, I cùng thuộc 1 đường tròn
b, Chứng minh AK.AI = AB.AC
cho đường tròn (O) từ A ở ngoài đường tròn vẽ hai tiếp tuyến AB và AC(B,C) là các tiếp điểm. OA cắt BC tại E. Gọi I là trung điểm BE, đường thẳng đi qua I và vuông góc OI cắt các tia AB,AC theo thứ tự tại D và F.chứng minh F là trung điểm BC
Cho tam giác ABC và một điểm I thuộc miền trong tam giác. Giả sử đường tròn ngoại tiếp tam giác IBC cắt các đoạn thẳng AB và AC lần lượt tại các điểm D và E. Gọi F là giao điểm của hai đường thẳng BE và CD. Đường thẳng ID và đường thẳng IE theo thứ tự cắt đường thẳng AF tại M và N.
1. Chứng minh rằng: đường tròn (C₁) ngoại tiếp tam giác BMN và đường tròn (C₂) ngoại tiếp tam giác CMN có độ dài bằng nhau.
2. Đường tròn (C₁) cắt đường thẳng AB và đường thẳng BE lần lượt tại P và T (P và T khác B). Đường tròn (C₂) cắt đường thẳng AC và đường thẳng CD lần lượt tại S và Q (S và Q khác C). Chứng minh rằng: ba đoạn thẳng MN, PQ và ST đồng qui tại trung điểm của mỗi đoạn.
Cho ba điểm A, B, C cố định nằm trên một đường thẳng và theo thứ tự đó. Đường tròn (O) thay đổi luôn đi qua B và C. Từ A kẻ các tiếp tuyến AM và AN với đường tròn (O) (M, N là hai tiếp điểm). Đường thẳng MN cắt AO tại H, gọi E là trung điểm của BC. Chứng minh rằng khi đường tròn (O) thay đổi, tâm của đường tròn ngoại tiếp tam giác OHE nằm trên một đường tròn cố định
Cho 2 đường tròn (O) và (O') cắt nhau ở A và B ( O và O' thuộc hai nửa mặt phẳng bờ AB). Một cát tuyến kẻ qua A cắt đường tròn (O) ở C, cắt đường tròn (O') ở D. Kẻ OM vuông góc với CD và O'N⊥ CD
a) CMR: MN = 1/2 CD
b) Gọi I là trung điểm của MN. CMR đường thẳng kẻ qua I vuông góc với BC đi qua 1 điểm cố định khi cắt tuyến CD kẻ qua A thay đổi
c) Qua A kẻ cát tuyến song song với đường nối tâm OO' cắt đường tròn (O) ở P, cắt đường tròn (O') ở Q. so sánh độ dài các đoạn PQ và CD