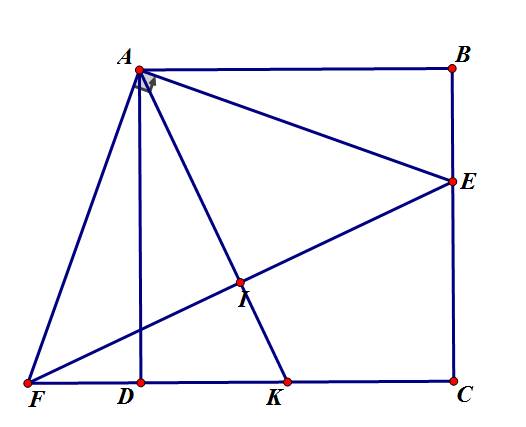
a) ΔADF và ΔABE có:
\(\widehat{ADF}=\widehat{ABE}=90^0\)
\(AD=AB\) (ABCD là hình vuông).
\(\widehat{DAF}=\widehat{BAE}\) (cùng phụ với \(\widehat{DAE}\))
\(\Rightarrow\)ΔADF=ΔABE (g-c-g)
\(\Rightarrow AE=AF\)
b) ΔFIK và ΔFCE có:
\(\widehat{FIK}=\widehat{FCE}=90^0\)
\(\widehat{CFE}\) là góc chung.
\(\Rightarrow\)ΔFIK=ΔFCE (g-g)
\(\Rightarrow\dfrac{FI}{FK}=\dfrac{FC}{FE}\Rightarrow FI.FE=FC.FK\left(1\right)\)
ΔAEF vuông cân tại A (\(AE\perp AF\) tại A, \(AE=AF\)) có:
AI là trung tuyến \(\Rightarrow\)AI là đường cao.
\(\Rightarrow AF^2=FK.FC\left(2\right)\)
\(\left(1\right),\left(2\right)\Rightarrow AF^2=FK.FC\)
c) \(BE=\dfrac{3}{4}BC=\dfrac{3}{4}AB=\dfrac{3}{4}.4=3\left(cm\right)\)
ΔABE vuông tại B có:
\(AE^2=AB^2+BE^2\)
\(\Rightarrow AE=\sqrt{AB^2+BE^2}=\sqrt{4^2+3^2}=5\left(cm\right)\)
- Vì ΔAEF vuông cân tại A:
\(\Rightarrow S_{AEF}=\dfrac{1}{2}AE^2=\dfrac{1}{2}.5^2=12,5\left(cm^2\right)\)












