Đáp án cần chọn là: D
Từ hình vẽ ta thấy các điểm E, H nằm bên ngoài tứ giác và điểm F nằm bên trong tứ giác ABCD nên D sai.
Đúng 0
Bình luận (0)
Các câu hỏi tương tự
Quan sát tứ giác ABCD ở hình 3 rồi điền vào chỗ trống: a) Hai đỉnh kề nhau: A và B, … Hai đỉnh đối nhau: A và C, … b) Đường chéo (đoạn thẳng nối hai đỉnh đối nhau): AC, … c) Hai cạnh kề nhau: AB và BC, … Hai cạnh đối nhau: AB và CD, … d) Góc: ∠A , … Hai góc đối nhau: ∠A và ∠C , … e) Điểm nằm trong tứ giác (điểm trong của tứ giác): M, … Điểm nằm ngoài tứ giác (điểm ngoài của tứ giác): N, …
Đọc tiếp
Quan sát tứ giác ABCD ở hình 3 rồi điền vào chỗ trống:
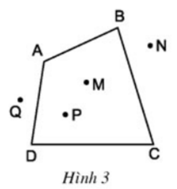
a) Hai đỉnh kề nhau: A và B, …
Hai đỉnh đối nhau: A và C, …
b) Đường chéo (đoạn thẳng nối hai đỉnh đối nhau): AC, …
c) Hai cạnh kề nhau: AB và BC, …
Hai cạnh đối nhau: AB và CD, …
d) Góc: ∠A , …
Hai góc đối nhau: ∠A và ∠C , …
e) Điểm nằm trong tứ giác (điểm trong của tứ giác): M, …
Điểm nằm ngoài tứ giác (điểm ngoài của tứ giác): N, …
Quan sát đa giác ABCDEG ở hình 119 rồi điền vào chỗ trống trong các câu sau: Các đỉnh là các điểm: A, B, … Các đỉnh kề nhau là: A và B, hoặc B và C, hoặc … Các cạnh là các đoạn thẳng: AB, BC, … Các đường chéo là các đoạn thẳng nối hai đỉnh không kề nhau: AC, CG, … Các góc là: ∠A , ∠B , … Các điểm nằm trong đa giác (các điểm trong của đa giác) là: M, N, … Các điểm nằm ngoài đa giác (các điểm ngoài của đa giác) là: Q, …
Đọc tiếp
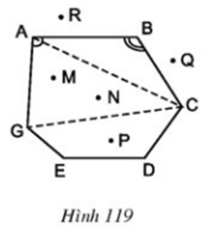
Quan sát đa giác ABCDEG ở hình 119 rồi điền vào chỗ trống trong các câu sau:
Các đỉnh là các điểm: A, B, …
Các đỉnh kề nhau là: A và B, hoặc B và C, hoặc …
Các cạnh là các đoạn thẳng: AB, BC, …
Các đường chéo là các đoạn thẳng nối hai đỉnh không kề nhau: AC, CG, …
Các góc là: ∠A , ∠B , …
Các điểm nằm trong đa giác (các điểm trong của đa giác) là: M, N, …
Các điểm nằm ngoài đa giác (các điểm ngoài của đa giác) là: Q, …
Cho hình chữ nhật ABCD với tâm đối xứng O. Từ các đỉnh A, C kẻ các đường vuông góc với đường chéo BD. Từ các đỉnh B, D kẻ các đường vuông góc với đường chéo AC, các đường vuông góc từ đỉnh A và B cắt nhau tại Q và các đường vuông góc từ đỉnh C và D cắt nhau tại N. Gọi M và P lần lượt là giao điểm của AQ với DN và BQ với CN. Chứng minh rằng:a) M và P đối xứng với nhau qua tâm O.b) Tứ giác MNPQ là hình thoi.
Đọc tiếp
Cho hình chữ nhật ABCD với tâm đối xứng O. Từ các đỉnh A, C kẻ các đường vuông góc với đường chéo BD. Từ các đỉnh B, D kẻ các đường vuông góc với đường chéo AC, các đường vuông góc từ đỉnh A và B cắt nhau tại Q và các đường vuông góc từ đỉnh C và D cắt nhau tại N. Gọi M và P lần lượt là giao điểm của AQ với DN và BQ với CN. Chứng minh rằng:
a) M và P đối xứng với nhau qua tâm O.
b) Tứ giác MNPQ là hình thoi.
Cho hình chữ nhật ABCD với tâm đối xứng O. Từ các đỉnh A, C kẻ các đường vuông góc với đường chéo BD. Từ các đỉnh B, D kẻ các đường vuông góc với đường chéo AC, các đường vuông góc từ đỉnh A và B cắt nhau tại Q và các đường vuông góc từ đỉnh C và D cắt nhau tại N. Gọi M và P lần lượt là giao điểm của AQ với DN và BQ với CN. Chứng minh rằng:a) M và P đối xứng với nhau qua tâm O.b) Tứ giác MNPQ là hình thoi.
Đọc tiếp
Cho hình chữ nhật ABCD với tâm đối xứng O. Từ các đỉnh A, C kẻ các đường vuông góc với đường chéo BD. Từ các đỉnh B, D kẻ các đường vuông góc với đường chéo AC, các đường vuông góc từ đỉnh A và B cắt nhau tại Q và các đường vuông góc từ đỉnh C và D cắt nhau tại N. Gọi M và P lần lượt là giao điểm của AQ với DN và BQ với CN. Chứng minh rằng:
a) M và P đối xứng với nhau qua tâm O.
b) Tứ giác MNPQ là hình thoi.
1, Cho tứ giác ABCD, các đường chéo AC và BD cắt nhau tại O. Các cạnh AD, BC kéo dài cắt nhau tại E. Biết AC vuông góc AD và BD vuông góc BC. Chứng minh rằng đường thẳng d đi qua các trung điểm OE và CD là trục đối xứng của cạnh AB2, Cho 2 điểm A, B nằm trên nửa mặt bờ là đường thẳng d. Gọi AH, BK là các đường vuông góc kẻ từ A, B đến d. Gọi C là điểm nằm bất kì giữa H và K, A đối xứng với A qua d, Giả sử góc ACH góc BCK a, Chứng minh rằng kí đó A , C , B thẳng hàng b, Nêu cách dựng điểm C sa...
Đọc tiếp
1, Cho tứ giác ABCD, các đường chéo AC và BD cắt nhau tại O. Các cạnh AD, BC kéo dài cắt nhau tại E. Biết AC vuông góc AD và BD vuông góc BC. Chứng minh rằng đường thẳng d đi qua các trung điểm OE và CD là trục đối xứng của cạnh AB
2, Cho 2 điểm A, B nằm trên nửa mặt bờ là đường thẳng d. Gọi AH, BK là các đường vuông góc kẻ từ A, B đến d. Gọi C là điểm nằm bất kì giữa H và K, A' đối xứng với A qua d, Giả sử góc ACH = góc BCK
a, Chứng minh rằng kí đó A' , C , B thẳng hàng
b, Nêu cách dựng điểm C sao cho AC + BC bé nhất
3, Cho tam giác ABC. Dựng hình đối xứng với tam giác đã cho qua trung điểm D của cạnh BC
a, Tứ giác tạo thành là hình gì
b, Tính chu vi tứ giác đó biết AB = 10cm, AC = 7cm
4, Cho hình bình hành với E, F lần lượt là trung điểm của AD, BC; G thuộc đoạn AB. Gọi H và I lần lượt là điểm đối xứng của G qua E và F
a, Chứng minh H, D, C, I thẳng hàng
b, Chưng minh HI = 2CD
tứ giác ABCD có đường chéo BD là trục đối xứng của hình. Đường phân giác góc ngoài tại đỉnh A và C cắt đường phân giác góc ngoài tại đỉnh B lần lượt E,F, cắt đường phân giác góc ngoài tại đỉnh D lần lượt tại H,G. CMR:
a)EFGH là hình thang cân
b) BD là trục đối xứng của hình thang EFGH
NHỜ 500 AE GIÚP MỀNH ZS .... NGÀY MAI PHẢI NỘP OY1. Cho tam giác ABC cân tại A có góc B60 độ, đường cao AM. Trên tia đối của tia MA lấy điểm E sao cho MEMAa) CM: Tứ giác ABEC là hình thoi và tính số đo góc BECb) Hai điểm D,E đối xứng nhau qua điểm C. Đường thẳng qua E song song với BC cắt AC tại F. Tứ giác ADFE là hình gì?Vì sao?c) CM: Tứ giác ABEF là hình thang când) Điểm C có là trực tâm của tam giác DBF không ? Giải thích?2. Cho tam giác ABC(ABAC), đoạn AI là đường cao và ba điểm D,E,F theo t...
Đọc tiếp
NHỜ 500 AE GIÚP MỀNH ZS .... NGÀY MAI PHẢI NỘP OY
1. Cho tam giác ABC cân tại A có góc B=60 độ, đường cao AM. Trên tia đối của tia MA lấy điểm E sao cho ME=MAa) CM: Tứ giác ABEC là hình thoi và tính số đo góc BEC
b) Hai điểm D,E đối xứng nhau qua điểm C. Đường thẳng qua E song song với BC cắt AC tại F. Tứ giác ADFE là hình gì?Vì sao?
c) CM: Tứ giác ABEF là hình thang cân
d) Điểm C có là trực tâm của tam giác DBF không ? Giải thích?
2. Cho tam giác ABC(AB<AC), đoạn AI là đường cao và ba điểm D,E,F theo thứ tự là trung điểm của các đoạn thẳng AB,AC,BC.a) CM: Tứ giác BDEF là hình bình hànhb) Điểm J là điểm dối xứng của điểm I qua điểm E. Tứ giác AICJ là hình gì? Vì sao?
b) Điểm J là điểm đối xứng của diểm I qua điểm E. Tứ giác AICJ là hình gì? Vì sao?
c) Hai đường thẳng BE,DF cắt nhau tại K. CM : Hai tứ giác ADKE và KECF có diện tích bằng nhau
d) Tính diện tích tam giác ADE theo diện tích tam giác ABC
3. Cho tam giác ABC cân tại A, trung tuyến AM. Gọi D là điểm đối xứng của A qua M. Gọi K là trung điểm của MC, E là điểm đối xứng của D qua K.a) CM: Tứ giác ABDC là hình thoi
b) CM: Tứ giác AMCE là hình chữ nhật
c) AM và BE cắt nhau tại I. CM : I là trung điểm của BE
d) CM: AK,CI,EM đồng quy
4. Cho hình chữ nhật ABCD(AB>AD), trên cạnh AD, BC lần lượt lấy các điểm M,N sao cho AM=CN.a) CMR: BM song song với DN
b) Gọi O là trung điểm của BD. CMR: AC,BD,MN đồng quy tại O
c) Qua O vẽ đường thẳng d vuông góc với BD, d cắt AB tại P, cắt CD tại Q. CMR : PBQD là hinh thoi
d) Đường thẳng qua B song song với PQ và đường thẳng qua Q song song với BD cắt nhau tại K. CMR : AC vuông góc với CK.
5. Cho tam giác ABC cân tại Acó M là trung điểm của cạnh BC . Gọi D là điểm đối xứng với A qua M.a) CM : Tứ giác ABDC là hình thoi
b) Vẽ đường thẳng vuông góc với BC tại B cắt tia CA tại điểm F. CM: Tứ giác ADBF là hình bình hành
c) Qua C vẽ đường thẳng song song với AD cắt tia BA tại điểm E. CM: Tứ giác BCEF là hình chữ nhật
d) Nối EM cắt AC tại N, kéo dài BN cắt EC tại I. CM: SIBC = 1/4 SBCEF
6. Cho hình chữ nhật ABCD có O là giao điểm của hai đường chéo . Lấy một điểm E nằm giữa hai điểm O và B. Gọi F là điểm đối xứng với điểm A qua E và I là trung điểm của CF.a) CM: Tứ giác OEFC là hình thang và tứ giác OEIC là hình bình hành
b) Gọi H và K lần lượt là hình chiếu của điểm F trên các đường thẳng BC và CD. CM: Tứ giác CHFK là hình chữ nhật và I là trung điểm của HK
c) CM: ba điểm E,H,K thẳng hàng
cho tam giác abc (ab khác ac , bc khác ac ) có đường cao bh ( h nằm giữa a và c ) . Gọi các điểm D, E , F lần lượt là trung điểm của các cạnh AB , AC và BC
A, tứ giác BDEF là hình gì ? vì sao
B , chứng minh hai điểm H và B đối xứng nhau qua DF
C,Tìm điều kiện của tam giác ABC để tứ giác BDEF là hình chứ nhật . Khi đó hãy tính diện tích tứ giác BDEF nếu AB = 3cm , DF = 2,5 cm
Cho tam giác ABC vuông tại A (AB < AC), đường cao AH. Vẽ hình vuông AHIK (điểm H nằm giữa hai điểm C và I), hai đường thẳng KI và AB cắt nhau tại D.
a) Chứng minh rằng AD = AC.
b) Vẽ hình bình hành ADEC có hai đường chéo cắt nhau tại O, chứng minh rằng ba điểm O, H, K cùng nằm trên đường trung trực của đoạn AI và tứ giác KOEI là hình thang.
Cho hình chữ nhật ABCD. O là giao điểm hai đường chéo và một điểm P bất kì trên đường chéo BD (P nằm giữa O và D). Gọi M là điểm đối xứng của C qua P. a) Chứng minh tứ giác AMDB là hình thang. Xác định vị trí của P trên BD để AMDB là hình thang cân. b) Kẻ ME vuông góc AD, MF vuông góc BA. Chứng minh EF // AC và 3 điểm E, F, P thẳng hàng. c) Xác định vị trí P trên BD để tứ giác nối 4 điểm A, M, D, B là hình thang cân. d) Nếu hình chữ nhật ABCD có AB 2BC. Gọi K là điểm trên AB sao cho góc ADK $1...
Đọc tiếp
Cho hình chữ nhật ABCD. O là giao điểm hai đường chéo và một điểm P bất kì trên đường chéo BD (P nằm giữa O và D). Gọi M là điểm đối xứng của C qua P. a) Chứng minh tứ giác AMDB là hình thang. Xác định vị trí của P trên BD để AMDB là hình thang cân. b) Kẻ ME vuông góc AD, MF vuông góc BA. Chứng minh EF // AC và 3 điểm E, F, P thẳng hàng. c) Xác định vị trí P trên BD để tứ giác nối 4 điểm A, M, D, B là hình thang cân. d) Nếu hình chữ nhật ABCD có AB = 2BC. Gọi K là điểm trên AB sao cho góc ADK = $15^o$. Chứng minh tam giác CDK cân.