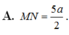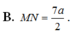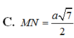
Ta có MPNQ là hình bình hành vì

Do đó
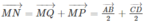
hay 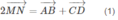
Mặt khác 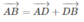
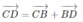
Nên
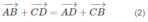
Vì

Từ (1) và (2) ta có:
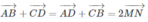
là đẳng thức cần chứng minh

Ta có MPNQ là hình bình hành vì

Do đó
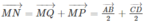
hay 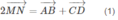
Mặt khác 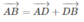
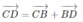
Nên
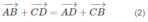
Vì

Từ (1) và (2) ta có:
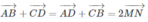
là đẳng thức cần chứng minh
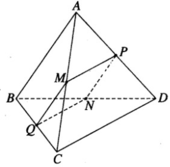
Cho hình tứ diện ABCD. Gọi M, N, P, Q lần lượt là trung điểm của các cạnh AC, BD, AD, BC. Chứng minh rằng: AB → - C D → = A C → B D → = 2 P Q →
Cho tứ diện ABCD có các cạnh AB,AC, AD vuông góc với nhau từng đôi một và AB=3a, AC=6a, AD=4a. Gọi M, N, P lần lượt là trung điểm các cạnh BC, CD, BD. Tính thể tích khối đa diện AMNP.
![]()
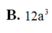
![]()
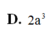
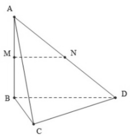
Cho tứ diện ABCD có các cạnh BA, BC, BD đôi một vuông góc với nhau: BA = 3a, BC =BD = 2a. Gọi M và N lần lượt là trung điểm của AB và AD Tính thể tích khối chóp C.BDNM.
A. V = 8 a 3
B. V = 2 a 3 3
C. V = 9 a 3 4
D. V = a 3
Cho tứ diện ABCD có các cạnh AB, AC, AD vuông góc với nhau từng đôi một và AB = 3cm, AC = 6cm, AD = 4cm. Gọi M, N, P lần lượt là trung điểm các cạnh BC, CD, DB. Tính thể tích khối đa diện AMNP.
A. 3 a 3
B. 12 a 3
C. a 3
D. 2 a 3
Trong không gian Oxyz, cho tứ diện ABCD với A(2;-4;6) và ba điểm B, C, D cùng thuộc mặt phẳng (Oyz). Gọi M, N, P lần lượt là trung điểm của AB, AC, AD. Lập phương trình mặt phẳng (MNP)
A. x + 1 = 0
B. x - 1 = 0
C. y + z - 1 = 0
D. x = 1 + t, y = -2, z = 3
II. Tự luận ( 5 điểm)
Cho tứ diện ABCD có các cạnh BA, BC, BD đôi một vuông góc với nhau:
BA = 3a, BC = BD = 2a. Gọi M và N lần lượt là trung điểm của AB và AD. Tính thể tích khối chóp C.BDNM
Cho khối tứ diện đều ABCD có thể tích là V. Gọi M, N, P, Q lần lượt là trung điểm của AC, AD, BD, BC. Thể tích khối chóp AMNPQ là:
A. V 6
B. V 3
C. V 4
D. V 2 3
Cho tứ diện ABCD có AC = 3a, B D = 4 a . Gọi M, N lần lượt là trung điểm của AD và BC. Biết AC vuông góc với BD. Tính MN
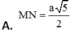
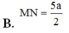
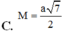
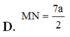
Cho tứ diện ABCD có A C = 3 a , B D = 4 a . Gọi M, N lần lượt là trung điểm của AD và BC. Biết AC vuông góc với BD. Tính MN.