Đáp án D
Ta có h = R
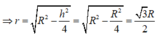
⇒ V t V c = πr 2 h 4 3 πR 3 = 9 16
Đáp án D
Ta có h = R
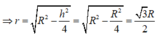
⇒ V t V c = πr 2 h 4 3 πR 3 = 9 16
Cho hình trụ nội tiếp mặt cầu thỏa mãn chiều cao của trụ
bằng bán kính mặt cầu. Gọi Vt , Vc lần lượt là thể tích của
hình trụ và hình cầu. Khi đó tỉ số thể tích V t V c bằng
![]()
![]()
![]()
Cho hình hộp A B C D . A ' B ' C ' D ' có A B = A D = 2 a , A A ' = 4 a Lấy M, N, P, Q lần lượt là trung điểm của A A ' , B B ' , C C ' , D D ' Biết hình hộp chữ nhật A B C D . A ' B ' C ' D ' nội tiếp khối trụ (T) và lăng trụ A B C D . M N P Q nội tiếp mặt cầu (C) Tỉ số thể tích V ( T ) V ( C ) giữa khối trụ và khối cầu là:
A. 2 3 3
B. 3 3
C. 2 3 3
D. 1 3 2
Cho hình hộp A B C D . A ' B ' C ' D ' có A B = A D = 2 a , A A ' = 4 a . Lấy M, N, P, Q lần lượt là trung điểm của AA’, BB’,CC, DD’. Biết hình hộp chữ nhật A B C D . A ' B ' C ' D ' nội tiếp khối trụ (T) và lăng trụ ABCD.MNPQ nội tiếp mặt cầu (C). Tỉ số thể tích V ( T ) V ( C ) giữa khối cầu và khối trụ là
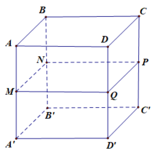
A. 2 3 3
B. 3 3
C. 2 3 3
D. 1 3 2
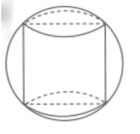
Một khối trụ tròn nội tiếp trong một mặt cầu (Hình vẽ), biết chiều cao hình trụ bằng bán kính mặt cầu, tính tỉ số k = V 1 V 2 với V 1 , V 2 lần lượt là thể tích khối trụ và mặt cầu
![]()
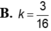
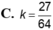
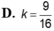
Khi cắt mặt cầu S(O;R) bởi một mặt kính, ta được hai nửa mặt cầu và hình tròn lớn của mặt kính đó gọi là mặt đáy của mỗi nửa mặt cầu. Một hình trụ gọi là nội tiếp nửa mặt cầu S(O;R) nếu một đáy của hình trụ nằm trong đáy của nửa mặt cầu, còn đường tròn đáy kia là giao tuyến của hình trụ với nửa mặt cầu. Biết R=1,tính bán kính đáy r và chiều cao h của hình trụ nội tiếp nửa mặt cầu S(O;R) để khối trụ có thể tích lớn nhất.
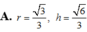
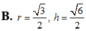
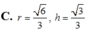
![]()
Khi cắt mặt cầu S(O;R) bởi một mặt kính, ta được hai nửa mặt cầu và hình tròn lớn của mặt kính đó gọi là mặt đáy của mỗi nửa mặt cầu. Một hình trụ gọi là nội tiếp nửa mặt cầu S(O;R) nếu một đáy của hình trụ nằm trong đáy của nửa mặt cầu, còn đường tròn đáy kia là giao tuyến của hình trụ với nửa mặt cầu. Biết R=1,tính bán kính đáy r và chiều cao h của hình trụ nội tiếp nửa mặt cầu S(O;R) để khối trụ có thể tích lớn nhất.
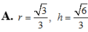
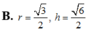
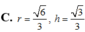
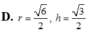
Cho mặt cầu (S) có bán kính bằng 4, hình trụ (H) có chiều cao bằng 4 và hai đường tròn đáy nằm trên Gọi V 1 là thể tích của khối trụ (H) và V 2 là thể tích của khối cầu (S). Tính tỉ số V 1 V 2 .
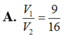
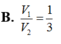
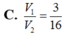
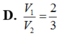
Khi cắt mặt cầu S (O, R) bởi một mặt kính đi qua tâm O, ta được hai nửa mặt cầu giống nhau. Giao tuyến của mặt kính đó với mặt cầu gọi là mặt đáy của mỗi nửa mặt cầu. Một hình trụ gọi là nội tiếp nửa mặt cầu S (O, R) nếu một đáy của hình trụ nằm trong đáy của nửa mặt cầu, còn đường tròn đáy kia là giao tuyến của hình trụ với nửa mặt cầu. Biết R = 1, tính bán kính đáy r và chiều cao h của hình trụ nội tiếp nửa mặt cầu S (O, R) để khối trụ có thể tích lớn nhất.
![]()
![]()
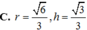
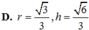
Cho hình trụ có bán kính đáy r, gọi O và O' là tâm của hai đường tròn đáy với OO'=2r. Một mặt cầu tiếp xúc với hai đáy của hình trụ tại O và O'. Gọi V C và V T lần lượt là thể tích của khối cầu và khối trụ. Khi đó V C V T bằng
![]()
![]()
![]()
![]()