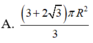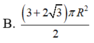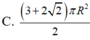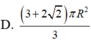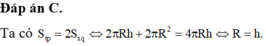Các câu hỏi tương tự
Cho hình trụ có chiều cao bằng 2a, bán kính đáy bằng a. Tính diện tích xung quanh của hình trụ Tính diện tích xung quanh của hình trụ A.
πa
2
B.
2
a
2
C. 2
πa
2
D. 4
πa
2
Đọc tiếp
Cho hình trụ có chiều cao bằng 2a, bán kính đáy bằng a. Tính diện tích xung quanh của hình trụ Tính diện tích xung quanh của hình trụ
A. πa 2
B. 2 a 2
C. 2 πa 2
D. 4 πa 2
Giả sử V là thể tích hình trụ tròn xoay với chiều cao h và bán kính đáy r. Chứng minh rằng với r là hằng số thì đạo hàm V'(h) bằng diện tích đáy hình trụ và với h là hằng số thì đạo hàm V'(r) bằng diện tích xung quanh của hình trụ.
Hình trụ có bán kính đáy r 5cm, chiều cao h7cm. Tính diện tích xung quanh của hình trụ.
Đọc tiếp
Hình trụ có bán kính đáy r =5cm, chiều cao h=7cm. Tính diện tích xung quanh của hình trụ.
![]()
![]()
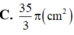
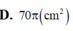
Cho hình trụ có bán kính đường tròn đáy bằng chiều cao và bằng 2cm. Diện tích xung quanh của hình trụ bằng
Đọc tiếp
Cho hình trụ có bán kính đường tròn đáy bằng chiều cao và bằng 2cm. Diện tích xung quanh của hình trụ bằng
![]()
![]()
![]()
![]()
Cho mặt cầu (S) có bán kính R. Một hình trụ có chiều cao h và bán kính đáy r thay đổi nội tiếp mặt cầu. Tính chiều cao h theo R sao cho diện tích xung quanh của hình trụ lớn nhất.
Đọc tiếp
Cho mặt cầu (S) có bán kính R. Một hình trụ có chiều cao h và bán kính đáy r thay đổi nội tiếp mặt cầu. Tính chiều cao h theo R sao cho diện tích xung quanh của hình trụ lớn nhất.
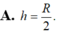
![]()
![]()
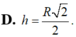
Một hình trụ có bán kính đáy bằng 3 và chiều cao bằng 4. Diện tích xung quanh của hình trụ là A. 36
π
B. 24
π
C. 42
π
D. 33
π
Đọc tiếp
Một hình trụ có bán kính đáy bằng 3 và chiều cao bằng 4. Diện tích xung quanh của hình trụ là
A. 36 π
B. 24 π
C. 42 π
D. 33 π
Trong không gian cho hình trụ có bán kính đáy R 3, chiều cao h 5. Tính diện tích toàn phần
S
t
p
của hình trụ đó. A.
S
t
p
48
π
B.
S
t
p
30
π
C.
S...
Đọc tiếp
Trong không gian cho hình trụ có bán kính đáy R = 3, chiều cao h = 5. Tính diện tích toàn phần S t p của hình trụ đó.
A. S t p = 48 π
B. S t p = 30 π
C. S t p = 18 π
D. S t p = 39 π
Cho hình cầu (S) tâm I, bán kính R không đổi. Một hình trụ có chiều cao h và bán kính đáy r thay đổi nội tiếp hình cầu. Tính chiều cao h theo R sao cho diện tích xung quanh của hình trụ lớn nhất A. h
R
2
B. h R C. h
R
2
D. h
R
2
2
Đọc tiếp
Cho hình cầu (S) tâm I, bán kính R không đổi. Một hình trụ có chiều cao h và bán kính đáy r thay đổi nội tiếp hình cầu. Tính chiều cao h theo R sao cho diện tích xung quanh của hình trụ lớn nhất
A. h = R 2
B. h =R
C. h = R 2
D. h = R 2 2
Một hình trụ có hai đường tròn đáy nằm trên một mặt cầu bán kính R và có đường cao bằng bán kính mặt cầu. Diện tích toàn phần hình trụ đó bằng
Đọc tiếp
Một hình trụ có hai đường tròn đáy nằm trên một mặt cầu bán kính R và có đường cao bằng bán kính mặt cầu. Diện tích toàn phần hình trụ đó bằng