Question

Cho hình thoi ABCD tâm O. Trên tia đối của các tia BA, CB, DC, AD lần lượt các điểm E, F, G, H sao cho BE = CF = DG = AH.

a) Chứng minh tứ giác EFGH là hình bình hành.

b) Chứng minh điểm O là tâm đối xứng của hình bình hành EFGH.

c) Hình thoi ABCD phải có điều kiện gì để EFGH trở thành hình thoi ?

Answer 1

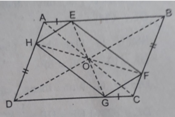
a) Ta có AB = CD (cạnh hình thoi)

BE = DG (gt)

⇒ AB + BE = CD + DG hay AE = CG (cmt)

Xét ΔAHE và ΔCFG có:

AE = CG

∠HAE = ∠FCG (cùng bù với ∠BAD = ∠DCB ),

AH = CF (gt)

Do đó ΔAHE = ΔCFG (c.g.c) ⇒ HE = FG

Chứng minh tương tự ta có HG = EF

Do đó tứ giác EFGH là hình bình hành (các cạnh đối bằng nhau).

b) Nối E và G.

Xét ΔOBE và ΔODG có

BE = DG (gt),

∠OBE = ∠ODG (so le trong),

OB = OD ( tính chất đường chéo của hình thoi ABCD)

⇒ ΔOBE = ΔODG (c.g.c) ⇒ ∠OBE = ∠ODG

Mà ∠DOG + ∠GOB = 180o ⇒ ba điểm G, O, E thẳng hàng.

Chứng minh tương tự ta có H, O, F thẳng hàng.

Vậy O là tâm đối xứng của hình bình hành EFGH.

c) Hình bình hành EFGH là hình thoi ⇔ HE = EF

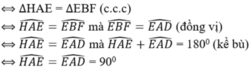
⇔ Hình thoi ABCD có 1 góc vuông

⇔ ABCD là hình vuông.

 

Vậy hình thoi ABCD phải là hình vuông thì hình bình hành EFGH trở thành hình thoi.