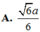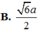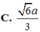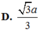
+) Vì ABCD là hình thang nên: CD // AB ⇒ CD// mp(SAB).
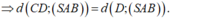
- Kẻ DH ⊥ SA.
+) Ta có:
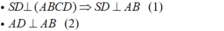
- Từ (1) và (2) suy ra:
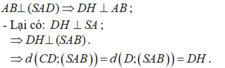
- Trong tam giác vuông SAD ta có:
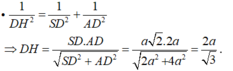

+) Vì ABCD là hình thang nên: CD // AB ⇒ CD// mp(SAB).
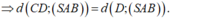
- Kẻ DH ⊥ SA.
+) Ta có:
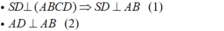
- Từ (1) và (2) suy ra:
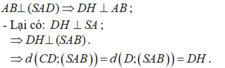
- Trong tam giác vuông SAD ta có:
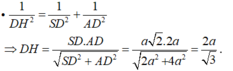
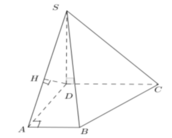
Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và D; SD vuông góc với mặt đáy (ABCD); AD=2a; S D = a 2 . Tính khoảng cách giữa đường thẳng CD và mặt phẳng (SAB).
A. 2 a 3
B. a 2
C. a 2
D. a 3 3
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB = a, AD = 2a, tam giác SAB cân tại S và nằm trong mặt phẳng vuông góc với đáy. Khoảng cách từ D đến (SBC) bằng 2 a 3 . Tính khoảng cách giữa hai đường thẳng SB và AC.
A . a 10 10
B . a 10 5
C . 2 a 10 5
D . 2 a 5 5
Cho hình chóp S. ABCD có đáy ABCD là hình thang vuông tại A và D, AD= DC = a . SAB là tam giác đều cạnh 2a và mặt phẳng (SAB) vuông góc với mặt phẳng (ABCD). Tính cosin của góc giữa hai mặt phẳng (SAB) và (SBC)
A. 2 7
B. 2 6
C. 3 7
D. 5 7
Cho hình chóp S.ABCD có đáy là hình chữ nhật, AB =a, AD = 2a. Tam giác SAB cân tại S và nằm trong mặt phẳng vuông góc với đáy. Góc giữa đường thẳng SC và mặt phẳng (ABCD) bằng 45 0 .Gọi M là trung điểm của SD. Tính theo a khoảng cách d từ điểm M đến mặt phẳng (SAC)
A. d = a 1315 89
B. d = a 1513 89
C. d = 2 a 1315 89
D. d = 2 a 1513 89
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật biết AB=a; AD= 2a; SA vuông góc với đáy, SA=a√2. Xác định và tính góc giữa. a) Các đường thẳng SB, SC, SD với mp đáy. b) SC với các mp (SAD) và ( SAB). c) SA với mp (SCD). d) SB và (SAC).
Cho hình vuông ABCD có tâm O ,cạnh 2a. Trên đường thẳng qua O và vuông góc với mp (ABCD) lấy điểm S. Biết góc giữa SA và (ABCD) bằng 45 0 . Độ dài SO bằng
A. S O = a 2
B. S O = 3 a
C. S O = 3 2 a
D. S O = 2 2 a
Cho hình thang ABCD vuông tại A và B, có AD = 2a, AB = BC = a. Trên tia Ax vuông góc với mặt phẳng (ABCD) lấy một điểm S. Gọi C', D' lần lượt là hình chiếu vuông góc ucar A trên SC và SD . Chứng minh rằng :
a) S B C ^ = S C D ^ = 90 o
b) AD’, AC’ và AB cùng nằm trên một mặt phẳng
c) Chứng minh rằng đường thẳng C’D’ luôn luôn đi qua một điểm cố định khi S di động trên tia Ax
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và D, AD=DC=a. Biết SAB là tam giác đều cạnh 2a và mặt phẳng (SAB) vuông góc với mặt phẳng (ABCD). Tính cosin của góc giữa hai mặt phẳng (SAB) và (SBC).
A. 2 7
B. 2 6
C. 3 7
D. 5 7
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B với AB=BC=a, AD=2a vuông góc với mặt phẳng đáy và SA=a. Tính theo a khoảng cách giữa hai đường thẳng AC và SD