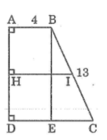
Gọi I là trung điểm của BC
Ta có: IB = IC = (1/2).BC = (1/2).13 = 6,5 (cm) (1)
Kẻ IH ⊥ AD. Khi đó HI là đường trung bình của hình thang ABCD.
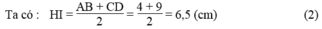
Từ (1) và (2) suy ra : IB = IH = R
Vậy đường tròn (I ; BC/2 ) tiếp xúc với đường thẳng AD

Gọi I là trung điểm của BC
Ta có: IB = IC = (1/2).BC = (1/2).13 = 6,5 (cm) (1)
Kẻ IH ⊥ AD. Khi đó HI là đường trung bình của hình thang ABCD.
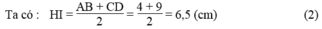
Từ (1) và (2) suy ra : IB = IH = R
Vậy đường tròn (I ; BC/2 ) tiếp xúc với đường thẳng AD
Cho hình thang vuông ABC
Cho hình thang vuông ABCD \(\left(\widehat{A}=\widehat{D}=90^0\right)\) , AB = 4cm, BC =13cm, CD = 9cm.
a, Tính độ dài AD
b, C/minh: Đường thẳng AD tiếp xúc với đường tròn đường kính BC.
c, Gọi H là tiếp điểm của đường thẳng AD với đường tròn đường kính BC. C/minh: BH là tia phân giác của góc ABC
d, Kẻ \(HK\perp BC\) tại K. C/minh: \(HK^2=AB.CD\) .
1)Cho tam giác đều ABC có đường cao AH. Trên cạnh BC lấy M bất kì. Từ M kẻ MP, MQ theo thứ tự vuông góc với AB, AC.
a) tìm tâm O của đường tròn ngoại tiếp tứ giác APMQ
b) CM: OH vuông góc với PQ.
2) Cho hình thang vuông( ^A=D=90o), AB=4cm, BC=13cm, CD= 9cm. Chứng minh rằng đường thẳng AD tiếp xúc với đường tròn có đường kính BC
Cho hình thang vuông ABCD ( ^A = ^D = 90°), AB = 4 cm, BC = 13cm,CD = 9 cm
a) Tính độ dài AD
b) C/m đường thẳng AD tiếp xúc với đường tròn đường kính BC
Cho hình thang vuông ABCD có A = D = 90 độ có BM = 90 độ với M là trung diểm của AD, chứng minh BC là tiếp tuyếncuar đường tròn đường kính AD
Cho hình thang vuông ABCD \(\left(\widehat{A}=\widehat{D}=90\right)\)có \(\widehat{BMC}=90\)với M là trung điểm của AD. Chứng minh rằng:
a) AD là tiếp tuyến của đường tròn có đường kính BC.
b) BC là tiếp tuyến của đường tròn có đường kính AD.
Cho hình thang vuông ABCD có ∠ A = ∠ D = 90 ° , AB = 4cm, BC = 13cm, CD = 9cm. Tính độ dài AD
Cho đường tròn tâm O, đường kính AB. Từ một điểm M trên nửa đường tròn , vẽ tiếp tuyến xy. Kẻ AD và BC cùng vuông góc vơi xy .
a) Chứng minh rằng : MC=MD
b) Chứng minh tổng AD+BC có giá trị không phụ thuộc vị trí điểm M trên nữa đường tròn tâm O
c) Chứng minh rằng : Đường tròn đường kính CD tiếp xúc với AB .
d) Xác định vị trí M để tứ giác ABCD có diện diện tích lớn nhất
Tứ giác ABCD có đường tròn (O) đường kính AB tiếp xúc CD. Chứng minh đường tròn (I) đường kính CD tiếp xúc AB <=>AD//BC.
Cho hình thang vuông ABCD (Góc A=D=90) có hai đường chéo vuông góc với nhau tại O, AB=4cm, CD= 9cm. Chứng minh AD^2= AB.CD, tính độ dài AD