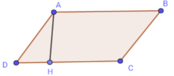
Ta có: SABCD = AH.CD = 6.12 = 72(cm2)
Đáp án cần chọn là: A

Ta có: SABCD = AH.CD = 6.12 = 72(cm2)
Đáp án cần chọn là: A
Cho hình bình hành ABCD có AB=4cm, đường cao AH ứng với cạnh CD=3cm
a Tính diện tích hình bình hành ABCD
b Gọi M là trung điểm cạnh AB. Tính diện tích tam giác AMD
c DN cắt AC tại N. Chứng minh DN=2MN
d Tính diện tích tam giác AMN
1. Cho hình thang ABCD có góc A=góc D=90độ. AC⊥Bd tại I. C/m:
a.ABD~DAC
b. Gọi E là hình chiếu của b xuống DC và BO=OD. C/m e điểm O,E,A thẳng hàng
c.Tỉ số diên tích AIB, DIC
2.Cho hình thang cân ABCD có AB//CD, AB<AC, đường chéo BD⊥cạnh bên BC, vẽ đường cao BH
a.BDC~HBC
b.Cho BC=15 cm, DC=25 cm. tính HC,HD
c.diện tích ABCD
Cho hình bình hành ABCD có CD = 16cm, đường cao vẽ từ A đến cạnh CD bằng 12cm.
a,Tính diện tích hình bình hành ABCD
b,gọi M là trung điểm AB. Tính diện tích tam giác ADM
c,DM cắt AC tại N. Chứng minh rằng DN = 2 NM
d, Tính diện tích tam giác AMN
Cho hình bình hàng ABCD (AB//CD), DC là đáy lớn AH là đường cao, M,N là trung điểm hai cạnh bên AD và BC
a) Chứng minh MNCH là hình bình hàng
b) Nếu DH = 5cm, AB = 10cm
Tính đường trung bình của hình thang ABCD trên
Cho hình bình hành ABCD,M 2 điểm bất kì trên cạnh BC.Trong nửa mặt phẳng bờ ABchứa c dựng hình vuông AMHN . Qua M dựng đường thẳng D song song với AB , d cắt AH ở E,cắt DC ở F.
a. Chứng minh rằng BM=ND
b. Chứng minh rằng:N;D;C thẳng hàn
c. EMFN là hình gì ?
d. chứng minh :DF+BM=FM và chu vi hình tam giác MFC không thay đổi
Cho hình bình hành ABCD, 2 đường chéo cắt nhau tại O. Trên BD lấy 2 điểm M và N sao cho BM=DN.
a) C/minh tứ giác AMCN là hình bình hành
b) An kéo dài cắt DC tại I và C M cắt AB tại K. C/minh I đối xứng với K qua O.
c) Tìm điều kiện của hình bình hành ABCD để AMCN là hình thoi.
d) Khi BM =DN = 1/3BD. Hãy c/minh K là trung điểm của AB và I là trung điểm của DC. Tính SBKM nếu SABCD =60 cm2
Cho hình bình hành ABCD. Đường phân giác ngoài của các góc tại các đỉnh A, B, C, D cắt nhau tại M, N, P, Q.
a) CMR: Tứ giác MNPQ là hình chữ nhật.
b) CMR: Hai đường chéo của hình chữ nhật MNPQ song song với hai cạnh của hình bình hành ABCD
c) Nếu ABCD là hình chưc nhật thì MNPQ là hình gì? Trong trường hợp này hãy tính diện tích của hình MNPQ biết các kích thước của hình chữ nhật ABCD là 6cm và 8cm
1) Cho hình chữ nhật ABCD có AB > AD. Vẽ AH vuông góc với BD tại điểm H.
a. Chứng minh △AHB và △BCD đồng dạng
b. Chứng minh BC.AB = AH.BD
c. Tia AH cắt cạnh DC tại M và cắt tia BC tại K. Chứng minh \(HA^2=HK.HM\)
2) Cho hình bình hành ABCD, trên tia đối của tia BA lấy BN = AD
a. Chứng minh: △CBN và △CDM cân
b. Chứng minh: △CBN \(\sim\) △MDN
c. Chứng minh: M,C,N thẳng hàng
3) Cho △ABC vuông tại A (AB < AC) có đường cao AH.
a. Chứng minh: △ABH\(\sim\)△CBA
b. Chứng minh: \(AH^2=BH.HC\)
c. Trên đường thẳng vuông góc với AC tại C, lấy điểm D sao cho CD=AB (D và B nằm khác phía so với đường thẳng AC). Đoạn thẳng HD cắt đoạn thẳng AC tại S. Kẻ \(\text{AF}\perp H\text{S }t\text{ại F}\)
Chứng minh BH.CH = HF.HD
Cho hình bình hành ABCD 2 đường chéo cắt nhau tại O. Trên BD lấy hai điểm M và N sao cho BM=DN
a/ C/minh AMCN là hình bình hành
b/ AN kéo dài cắt DC tại I và CM kéo dài cắt AB tại K. Cmr I đối xứng với K qa O
C/ Tìm điều kiện của hbh ABCD để AMCN là hình thoi
d/ Khi BM=DN=1/3 BD. Hãy c/minh K là trung điểm AB và I là trung điểm DC. Tính diện tích BKM nếu diện tích ABCD=60cm2