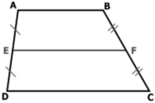
Ta có hình thang ABCD có E là trung điểm của AD, F là trung điểm của BC
⇒ EF là đường trung bình của hình thang.
Áp dụng định lý 2, ta có EF = (AB + CD)/2
⇒ EF = (AB + CD)/2 = (4 + 7)/2 = 5,5( cm ).
Cho hình thang ABCD có AB//CD và AB=AB=16cm; BC=30cm; CD =50 cm Gọi E,F là trung điểm của AB,CD.Tính độ dài đoạn thẳng EF
cho hình thang ABCD (AB// CD) có AB= 7,5 cm , CD=12cm. Gọi M là trung điểm của CD. E là giao điểm của MA và BD. F là giao điểm của AC và BM.
chứng minh: EF//AB
tính độ dài đoạn thẳng EF
a, cho hình thanh ABCD(AB//CD). Gọi E,F lần lượt là trung điểm AD Và BC.
Biết AB=8cm: CD=12cm. Tính độ dài EF.
b, Cho hình thang ABCD(AB//CD). Gọi E,F lần lượt là trung điểm AD và BC.
Biết AB=10cm: EF=16cm. Tính độ dài CD.
Cho hình thang ABCD (AB//CD) có AB=7.5cm ; CD=12cm. Gọi M là trung điểm của CD ; E là giao điểm của MA và BD ; F là giao điểm của MB và AC
a) CM: EF//AB
b) Tính độ dài EF
cho hình thang ABCD (ab/cd) có AB =12 cm. E là trung điểm của AD, F là trung điểm của BC
a) biết EF =13cm. tính CD
b) AC cắt EF tại M. Tính EM,MF
Cho hình thang ABCD ( AB // CD ), E là trung điểm của AD, F là trung điểm BC. EF cắt BD ở I, cắt AC ở K.
a, CMR AK=KC, BI=ID.
b, Cho AB = 6 cm, CD = 10 cm. Tính độ dài EI, KF, IK.
1) Cho tam giác ABC, điểm I thuộc đường trung tuyến AM. Gọi E là giao điểm của BI và AC, F là giao điểm của CI và AB. G là trung điểm BF, H là trung điểm CE. CMR: EF//BC
2) Cho hình thang ABCD (AB//CD) có AB=12, CD=15. Gọi M là trung điểm AB, E là giao điểm CM và AD, F là giao điểm của DM và BC. Tính độ dài EF
3) Cho hình bình hành ABCD, E thuộc AD, F thuộc AB, I thuộc AC. Gọi M là giao điểm FI và CD, K là giao điểm EI và BC. CMR: MK//EF
4) Cho tam giác ABC, AB=10, AC=15, 1 đường thẳng đi qua điểm M thuộc cạnh AB và song song với BC cắt AC ở N sao cho AN=BM. Tính độ dài AM sao cho AM=BN
5) Cho tam giác ABC có AB<AC, đường phân giác AD, lấy I thuộc BC sao cho BI=2 IC. Qua I kẻ đường thẳng song song với AD cắt AC và AB theo thứ tự ở E và K. CM BK= 2 CE
CHo hình thang ABCD : có 2 đáy là AB và CD. M là trung điểm CD, E là giao điểm của MA và BD, F là giao điểm của MB và Ac.
a) CM : EF // AB
b) EF cắt AD và BC lần lượt tại H và N . CM : HE=EF=FN.
Cho hình thang ABCD. Biết rằng E là trung điểm của AD, F là trung điểm của BC. Đường thẳng EF cắt DB ở G, cắt AC ở H. Độ dài đoạn AB = 30cm, DC = 50cm. EG =? cm GH = cm? HF = ?cm
