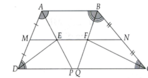
Cho hình thang ABCD (AB//CD) với AB = a, BC = b, CD = c và DA = d. Các tia phân giác của góc A và góc D cắt nhau tại E, các tia phân giác của B ^ và C ^ cắt nhau tại F. Gọi M, N theo thứ tự là trung điểm của AD và BC.
a) Chứng minh M, E, N, F cùng nằm trên một đường thẳng.
b) Tính độ dài MN, MF, FN theo a, b, c, d.
a) Gọi P và Q lần lượt là giao điểm của AE, AF với CD.
Chứng minh tương tự 2B.
b) Ta có:
M N = 1 2 ( A B + C D ) = 1 2 ( a + c )
Lại có:
c = CD = CQ + QD = BC + QD = b + QD (do tam giác BCQ cân) Þ QD = c - b.
Trong hình thang ABQD có M là trung điểm của AD và MF//DQ nên chứng minh được F là trung điểm của BQ, từ đó chứng minh MF là đường trung bình của hình thang ABQD.
Vì MF là đường trung bình của hình thang ABQD.
Þ M F = 1 2 ( A B + D Q ) = 1 2 ( a + c − b )
Mặt khác, FN là đường trung bình của tam giác BCQ, tức là F N = 1 2 C Q = 1 2 b .