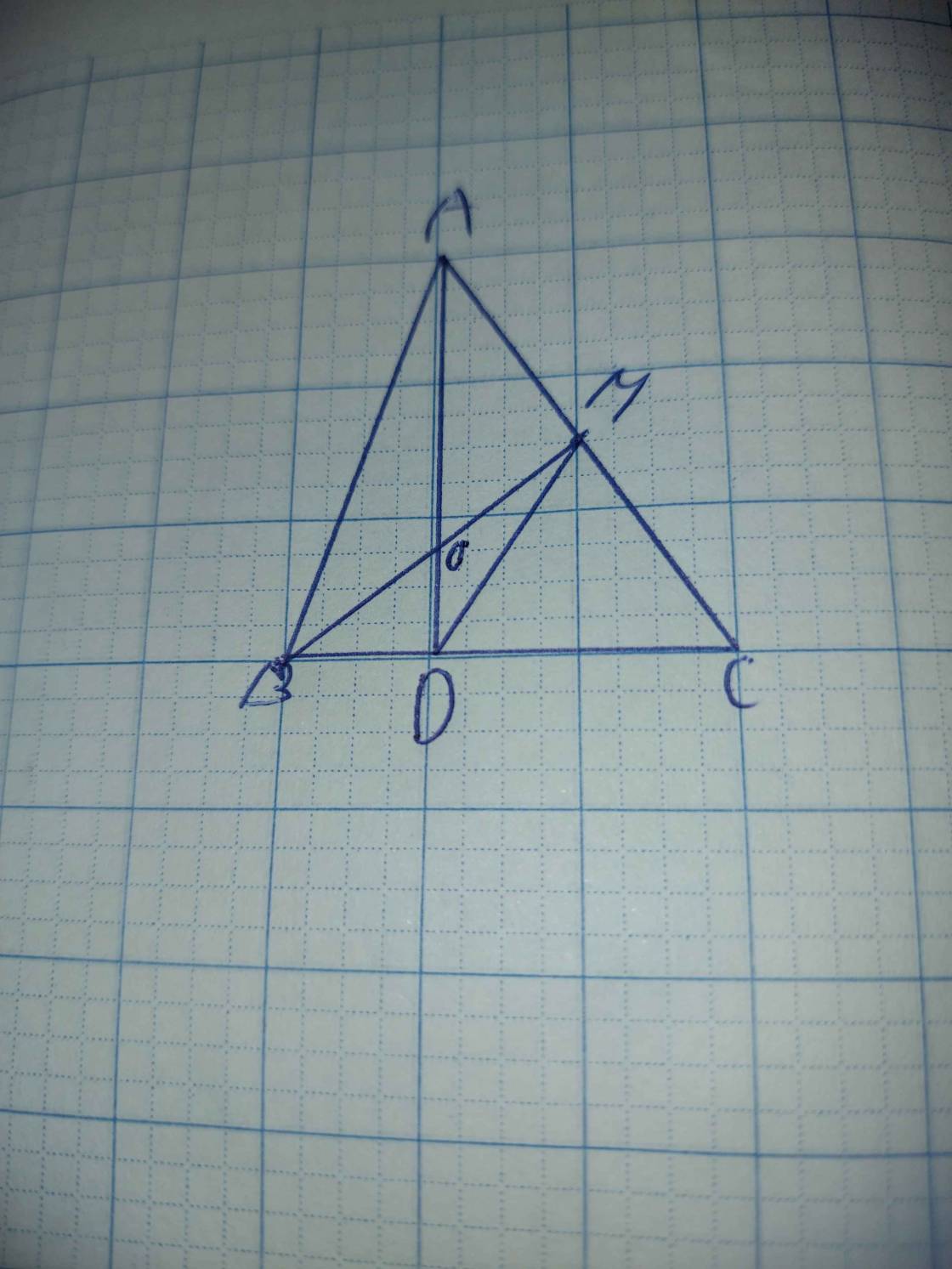Question

Cho hình tam giác ABC,M là trung điểm của AC,D là điểm trên BC sao cho BD=1/3 BC 

a. Tính diện tích tam giác ABC biết diện tích ABD là 12 cm² 

b. So sánh diện tích ABD, diện tích ADM và diện tích DMC

c. Nối BM cắt AD tại O. So sánh BO và OM

Answer 1

hình vẽ cậu tự vẽ nha

a)nối a với d 

theo hình vẽ , ta có diện tích tam giác diện tích tam giác abd = \(\frac{1}{3}\)diện tích tam giác abc vì :

chung chiều cao hạ từ đỉnh a xuống cạnh đáy bc , bd = \(\frac{1}{3}\)bc ; vậy diện tích tam giác abd là

               12 x \(\frac{1}{3}\)= 4 (cm²)

b) vì diện tích tam giác abd =4cm² nên diện tích tam giác acd là : 

                12 - 4 = 8 (cm²)

 vậy diện tích tam giác adm và mcd sẽ bằng 4 cm² vì chung chiều cao hạ từ đỉnh d xuống cạnh đáy ac ; am = mc

vì vậy nên diện tích của cả 3 hình tam giác bằng nhau và bằng  4cm²

c) trong toán học diện tích và chiều cao là 2 đại lượng tỉ lệ thuận nên hình tam giác có chung chiều cao nhưng diện tích lớn hơn thì cạnh đáy sễ lớn hơn.

phần c) tớ chỉ giúp đc đến đấy thôi, mong cậu thông cảm

              

Answer 2

Hình nè  

Answer 3

a)nối a với d 

theo hình vẽ , ta có diện tích tam giác diện tích tam giác abd = 1331​diện tích tam giác abc vì :

chung chiều cao hạ từ đỉnh a xuống cạnh đáy bc , bd = 1331​bc ; vậy diện tích tam giác abd là

               12 x 1331​= 4 (cm2)

b) vì diện tích tam giác abd =4cm2 nên diện tích tam giác acd là : 

                12 - 4 = 8 (cm2)

 vậy diện tích tam giác adm và mcd sẽ bằng 4 cm2 vì chung chiều cao hạ từ đỉnh d xuống cạnh đáy ac ; am = mc

vì vậy nên diện tích của cả 3 hình tam giác bằng nhau và bằng  4cm2

c) trong toán học diện tích và chiều cao là 2 đại lượng tỉ lệ thuận nên hình tam giác có chung chiều cao nhưng diện tích lớn hơn thì cạnh đáy sễ lớn hơn.