Các câu hỏi tương tự
Cho hình nón đỉnh (S) có đường sinh bằng 2 , đường cao bằng 1 . Tìm đường kính của mặt cầu chứa điểm S và chứa đường tròn đáy hình nón đã cho:
Đọc tiếp
Cho hình nón đỉnh (S) có đường sinh bằng 2 , đường cao bằng 1 . Tìm đường kính của mặt cầu chứa điểm S và chứa đường tròn đáy hình nón đã cho:
![]()
![]()
![]()
![]()
Cho hình nón có đường sinh bằng 2 và diện tích xung quanh bằng
2
3
π
. Tìm đường kính của mặt cầu chứa điểm S và chứa đường tròn đáy hình nón đã cho
Đọc tiếp
Cho hình nón có đường sinh bằng 2 và diện tích xung quanh bằng 2 3 π . Tìm đường kính của mặt cầu chứa điểm S và chứa đường tròn đáy hình nón đã cho
![]()
![]()
![]()
![]()
Cho
S
:
x
2
+
y
-
1
2
+
z
+
1
2
8
và
A
2
;
3
;
-
1...
Đọc tiếp
Cho S : x 2 + y - 1 2 + z + 1 2 = 8 và A 2 ; 3 ; - 1 . Xét mặt nón tròn xoay đỉnh A trục là IA( I là tâm mặt phẳng (S)) với góc ở đỉnh bằng 120 0 , đường tròn đáy hình nón thuộc mặt cầu. Viết phương trình mặt phẳng (P) chứa đường tròn đáy hình nón.
![]()
![]()
![]()
![]()
Cho hình nón đỉnh S có chiều cao h a và bán kính đáy r 2a. Mặt phẳng (P) đi qua S, không chứa trục của hình nón cắt đường tròn đáy tại A và B sao cho AB
2
3
a
.Khoảng cách từ âm của hình tròn đáy đến mặt phẳng (P) bằng
Đọc tiếp
Cho hình nón đỉnh S có chiều cao h = a và bán kính đáy r = 2a. Mặt phẳng (P) đi qua S, không chứa trục của hình nón cắt đường tròn đáy tại A và B sao cho AB = 2 3 a .Khoảng cách từ âm của hình tròn đáy đến mặt phẳng (P) bằng

![]()
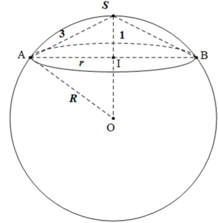
Cho hình cầu (S) tâm O, bán kính R. Hình cầu (S) ngoại tiếp một hình trụ tròn xoay (T) có đường cao bằng đường kính đáy và hình cầu (S) lại nội tiếp trong một nón tròn xoay (N) có góc ở đỉnh bằng
60
°
. Tính tỉ số thể tích của hình trụ (T) và hình nón (N).
Đọc tiếp
Cho hình cầu (S) tâm O, bán kính R. Hình cầu (S) ngoại tiếp một hình trụ tròn xoay (T) có đường cao bằng đường kính đáy và hình cầu (S) lại nội tiếp trong một nón tròn xoay (N) có góc ở đỉnh bằng 60 ° . Tính tỉ số thể tích của hình trụ (T) và hình nón (N).
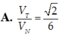
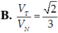
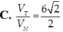
![]()
Cho hình cầu (S) tâm O, bán kính R. Hình cầu (S) ngoại tiếp một hình trụ tròn xoay (T) có đường cao bằng đường kính đáy và hình cầu (S) lại nội tiếp trong một hình nón tròn xoay (N) có góc ở đỉnh bằng
60
°
. Tính tỉ số thể tích của hình trụ (N) và hình nón (T). A.
V
T
V
N
2
6
B...
Đọc tiếp
Cho hình cầu (S) tâm O, bán kính R. Hình cầu (S) ngoại tiếp một hình trụ tròn xoay (T) có đường cao bằng đường kính đáy và hình cầu (S) lại nội tiếp trong một hình nón tròn xoay (N) có góc ở đỉnh bằng 60 ° . Tính tỉ số thể tích của hình trụ (N) và hình nón (T).
A. V T V N = 2 6
B. V T V N = 2 3
C. V T V N = 3 2
D. Đáp án khác
Cho mặt cầu (S) tâm O bán kính r. Hình nón có đường tròn đáy (C) và đỉnh I thuộc (S) được gọi là hình nón nội tiếp mặt cầu (S). Gọi h là chiều cao của hình nón đó. Thể tích của khối nón theo r và h.
II. Tự luận ( 4 điểm)
Cho hình nón tròn xoay có đỉnh là S, O là tâm của đường tròn đáy, đường sinh bằng a 2 và góc giữa đường sinh và mặt phẳng đáy bằng 60°. Diện tích xung quanh S x q của hình nón và thể tích V của khối nón tương ứng là:
Cho mặt cầu (S) tâm O bán kính r. Hình nón có đường tròn đáy (C) và đỉnh I thuộc (S) được gọi là hình nón nội tiếp mặt cầu (S). Gọi h là chiều cao của hình nón đó. Xác định h để thể tích của hình nón là lớn nhất.