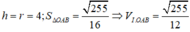Các câu hỏi tương tự
Cho hình nón tròn xoay đỉnh S, đáy là một hìnht tròn tâm O bán kính R, chiều cao của hình nón bằng 2R. Gọi I là một điểm nằm trên mặt phẳng đáy sao cho IO 2R. Giả sử A là điểm trên đường tròn (O) sao cho OA
⊥
OI. Diện tích xung quanh của hình nón bằng:
Đọc tiếp
Cho hình nón tròn xoay đỉnh S, đáy là một hìnht tròn tâm O bán kính R, chiều cao của hình nón bằng 2R. Gọi I là một điểm nằm trên mặt phẳng đáy sao cho IO = 2R. Giả sử A là điểm trên đường tròn (O) sao cho OA ⊥ OI. Diện tích xung quanh của hình nón bằng:
![]()
![]()
![]()
![]()
Cho hình nón đỉnh S với đáy là đường tròn tâm O bán kính R. Gọi I là một điểm nằm trên mặt phẳng đáy sao cho OI R
3
. Giả sử A là điểm nằm trên đường tròn (O; R) sao cho OA ⊥ OI. Biết rằng tam giác SAI vuông cân tại S. Khi đó, diện tích xung quanh
S
xq
của hình nón và thể tích V của khối nón là: A.
S
xq
πR
2
;...
Đọc tiếp
Cho hình nón đỉnh S với đáy là đường tròn tâm O bán kính R. Gọi I là một điểm nằm trên mặt phẳng đáy sao cho OI = R 3 . Giả sử A là điểm nằm trên đường tròn (O; R) sao cho OA ⊥ OI. Biết rằng tam giác SAI vuông cân tại S. Khi đó, diện tích xung quanh S xq của hình nón và thể tích V của khối nón là:
A. S xq = πR 2 ; V = πR 3 3
B. S xq = 2 πR 2 ; V = 2 πR 3 3
C. S xq = πR 2 2 2 ; V = πR 3 6
D. S xq = πR 2 ; V = 2 πR 3 3
Cho hình nón đỉnh S có đáy là đường tròn tâm O và bán kính R. Trên đường tròn (O) lấy 2 điểm A, B sao cho tam giác OAB vuông. Biết diện tích tam giác SAB bằng
R
2
2
, thể tích khối nón đã cho bằng
Đọc tiếp
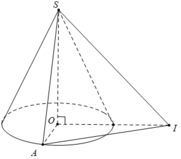
Cho hình nón đỉnh S có đáy là đường tròn tâm O và bán kính R. Trên đường tròn (O) lấy 2 điểm A, B sao cho tam giác OAB vuông. Biết diện tích tam giác SAB bằng R 2 2 , thể tích khối nón đã cho bằng
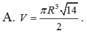
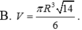
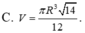
![]()
Cho hình nón đỉnh S có đáy là đường tròn tâm O, bán kính R. Trên đường tròn (O) lấy 2 điểm A, B sao cho tam giác OAB vuông. Biết diện tích tam giác SAB bằng
R
2
2
, thể tích khối nón đã cho bằng
Đọc tiếp
Cho hình nón đỉnh S có đáy là đường tròn tâm O, bán kính R. Trên đường tròn (O) lấy 2 điểm A, B sao cho tam giác OAB vuông. Biết diện tích tam giác SAB bằng R 2 2 , thể tích khối nón đã cho bằng
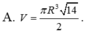
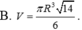
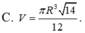
Cho hình trụ có đáy là hai đường tròn tâm O và O’, bán kính đáy bằng chiều cao và bằng 2a. Trên đường tròn đáy có tâm O lấy điểm A, D sao cho
A
D
2
3
a
; gọi C là hình chiếu vuông góc của D lên mặt phẳng chứa đường tròn (O’); trên đường tròn tâm O’ lấy điểm B (AB chéo với CD) . Đặt
α
là...
Đọc tiếp
Cho hình trụ có đáy là hai đường tròn tâm O và O’, bán kính đáy bằng chiều cao và bằng 2a. Trên đường tròn đáy có tâm O lấy điểm A, D sao cho A D = 2 3 a ; gọi C là hình chiếu vuông góc của D lên mặt phẳng chứa đường tròn (O’); trên đường tròn tâm O’ lấy điểm B (AB chéo với CD) . Đặt α là góc giữa AB và đáy. Tính tan α khi thể tích khối tứ diện CDAB đạt giá trị lớn nhất.
A. tan α = 3
B. tan α = 1 2
C. tan α = 1
D. tan α = 3 3
Cho hình nón đỉnh S, đường cao SO. Gọi A và B là hai điểm thuộc đường tròn đáy của hình nón sao cho khoảng cách từ O đến AB bằng 2 và . Tính diện tích xung quanh hình nón ? A.
4
π
3
B.
3
π
2
4
C.
2
π
3
D.
3
π
2
Đọc tiếp
Cho hình nón đỉnh S, đường cao SO. Gọi A và B là hai điểm thuộc đường tròn đáy của hình nón sao cho khoảng cách từ O đến AB bằng 2 và ![]() . Tính diện tích xung quanh hình nón ?
. Tính diện tích xung quanh hình nón ?
A. 4 π 3
B. 3 π 2 4
C. 2 π 3
D. 3 π 2
Cho hình nón đỉnh S có đáy là đường tròn tâm O, bán kính R. Trên đường tròn (O) lấy hai điểm A, B sao cho tam giác OAB vuông. Biết diện tích tam giác SAB bằng
R
2
2
, thể tích hình nón đã cho bằng
Đọc tiếp
Cho hình nón đỉnh S có đáy là đường tròn tâm O, bán kính R. Trên đường tròn (O) lấy hai điểm A, B sao cho tam giác OAB vuông. Biết diện tích tam giác SAB bằng R 2 2 , thể tích hình nón đã cho bằng
![]()
![]()
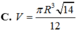
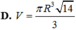
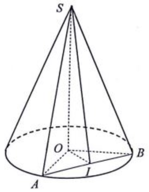
Cho hình nón đỉnh S có đáy là đường tròn tâm O bán kính R. Trên đường tròn (O) lấy hai điểm A, B sao cho tam giác OAB vuông. Biết diện tích tam giác SAB bằng
R
2
2
. Thể tích hình nón đã cho bằng
Đọc tiếp
Cho hình nón đỉnh S có đáy là đường tròn tâm O bán kính R. Trên đường tròn (O) lấy hai điểm A, B sao cho tam giác OAB vuông. Biết diện tích tam giác SAB bằng R 2 2 . Thể tích hình nón đã cho bằng
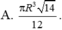
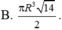
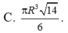
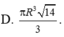
Một hình nón tròn xoay có đỉnh là D, tâm của đường tròn đáy là O, đường sinh bằng l và có góc giữa đường sinh và mặt phẳng đáy bằng
α
. Gọi I là một điểm trên đường cao DO của hình nón sao cho
DI
DO
k (0 k 1) . Tính diện tích thiết diện qua I và vuông góc với trục của hình nón.
Đọc tiếp
Một hình nón tròn xoay có đỉnh là D, tâm của đường tròn đáy là O, đường sinh bằng l và có góc giữa đường sinh và mặt phẳng đáy bằng α . Gọi I là một điểm trên đường cao DO của hình nón sao cho DI DO = k (0 < k < 1) . Tính diện tích thiết diện qua I và vuông góc với trục của hình nón.