Đáp án C
Theo giả thiết R = a 3 2
Vậy diện tích mặt cầu là 4 πR 2 = 3 a 2
Đáp án C
Theo giả thiết R = a 3 2
Vậy diện tích mặt cầu là 4 πR 2 = 3 a 2
Cho hình lập phương cạnh a. Diện tích mặt cầu đi qua các đỉnh của hình lập phương là
A. a 2
B. 2 a 2
C. 3 a 2
D. 4 a 2
Cho hình lập phương ABCD.A’B’C’D’ cạnh a. Tính diện tích mặt cầu đi qua tất cả các đỉnh của hình lập phương.
Cho hình lập phương có cạnh bằng a và một hình trụ có hai đáy là hai hình tròn nội tiếp hai mặt đối diện của hình lập phương. Gọi S 1 là diện tích 6 mặt của hình lập phương, S 2 là diện tích xung quanh của hình trụ. Tỉ số S 2 / S 1 bằng:
A. π /6 B. 1/2
C. π /2 D. π
Cho hình lập phương có cạnh bằng 1. Thể tích của mặt cầu đi qua các đỉnh hình lập phương là
![]()
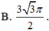
![]()
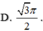
Cho hình lập phương ABCD.A'B'C'D' có độ dài mỗi cạnh là 10cm. Gọi O là tâm mặt cầu đi qua 8 đỉnh của hình lập phương. Khi đó, diện tích S của mặt cầu là:
A. S = 150 π cm 2
B. S = 100 3 π cm 2
C. S = 300 π cm 2
D. S = 250 π cm 2
Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng a. Hãy xác định tâm và bán kính mặt cầu:
Đi qua 8 đỉnh của hình lập phương.
Mặt cầu đi qua tất cả các đỉnh của hình lập phương cạnh a có bán kính bằng
![]()
![]()
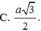
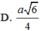
Trong không gian Oxyz, cho hình lập phương ABCD.A'B'C'D' có tọa độ các đỉnh A(0;0;0), B(1;0;0), C(0;1;0) và A’(0;0;1). Gọi M là trung điểm cạnh AB và N là tâm của hình vuông ADD'A' Diện tích của thiết diện tạo bởi mặt phẳng (CMN) và hình lập phương đã cho bằng
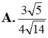
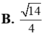
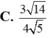
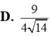
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a. Diện tích S của mặt cầu ngoại tiếp hình lập phương đó là:
![]()
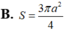
![]()
![]()