Đáp án B
![]()
![]()
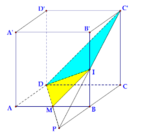
Dễ dàng chứng minh B, M lần lượt là trung điểm PC và AB
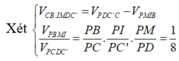
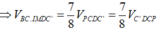
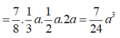
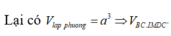
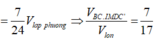
Đáp án B

![]()
![]()
Dễ dàng chứng minh B, M lần lượt là trung điểm PC và AB
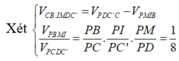
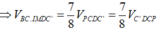
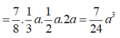
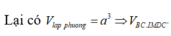
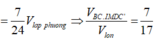
Cho hình lập phương ABCD.A' B'C' D' cạnh bằng a và K là một điểm nằm trên cạnh CC’ sao cho C K = 2 a 3 . Mặt phẳng ( α ) qua A, K và song song với BD chia khối lập phương thành hai phần có thể tích V 1 V 2 ( V 1 < V 2 ) . Tính tỉ số V 1 V 2
A. V 1 V 2 = 1 4
B. V 1 V 2 = 1 2
C. V 1 V 2 = 2 3
D. V 1 V 2 = 1 3
Cho khối lập phương ABCD.A’B’C’D’ cạnh a. Các điểm E và F lần lượt là trung điểm của C’B’ và C’D’. Mặt phẳng (AEF) cắt khối lập phương đã cho thành hai phần, gọi V 1 là thể tích khối chứa điểm A’ và V 2 là thể tích khối chứa điểm C’. Khi đó V 1 V 2 là.
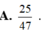
![]()
![]()
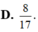
Cho hình lăng trụ tam giác ABC.A'B'C'. Gọi M,N lần lượt là trung điểm của BB', CC'. Mặt phẳng (A'MN) chia khối lăng trụ thành hai phần, V 1 là thể tích của phần đa diện chứa điểm B, V 2 thể tích phần đa diện còn lại. Tính tỉ số V 1 V 2
A. V 1 V 2 = 7 2
B. V 1 V 2 = 2
C. V 1 V 2 = 3
D. V 1 V 2 = 5 2
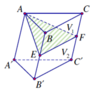
Cho hình lăng trụ ABC.A'B'C'. Gọi E, F lần lượt là trung điểm của BB' và CC'. Mặt phẳng (AEF) chia khối lăng trụ thành hai phần có thể tích V 1 và V 2 như hình vẽ. Tỉ số V 1 V 2 là
A. 1
B. 1 3
C. 1 4
D. 1 2
Cho hình lăng trụ ABC.A'B'C' Gọi E, F lần lượt là trung điểm của BB¢ và CC¢. Mặt phẳng (AEF) chia khối lăng trụ thành hai phần có thể tích V 1 và V 2 như hình vẽ.
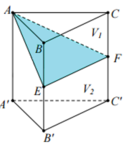
Tỉ số V 1 V 2 là
A. 1 2
B. 1
C. 1 3
D. 1 4
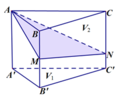
Cho khối lăng trụ ABC.A'B'C' . Gọi M là trung điểm của BB' , N là điểm trên cạnh CC' sao cho CN = NC’. Mặt phẳng ( AMN ) chia khối lăng trụ thành hai phần có thể tích V 1 và V 2 như hình vẽ. Tính tỉ số V 1 V 2
A. V 1 V 2 = 5 3
B. V 1 V 2 = 3 2
C. V 1 V 2 = 4 3
D. V 1 V 2 = 7 5
Cho hình chóp tứ diện đều S.ABCD có canh đáy a, cạnh bên hợp với đáy một góc 60 o . Gọi M là điểm đối xứng với C qua D, N là trung điểm của SC, mặt phẳng (BMN) chia khối chóp S.ABCD thành 2 phần. Tính tỉ số thể tích của hai phần đó.
A. 7 5
B. 7 3
C. 1 7
D. 1 5
Cho lăng trụ ABC.A'B'C' trên các cạnh AA’, BB’ lấy các điểm M, N sao cho AA' = 3A'M, BB' = 3B'N. Mặt phẳng (C'MN) chia khối lăng trụ đã cho thành hai phần. Gọi V 1 là thể tích của khối chóp C'.A'B'MN, V 2 là thể tích của khối đa diện ABCMNC'. Tỉ số V 1 V 2 bằng:
A. V 1 V 2 = 4 7
B. V 1 V 2 = 2 7
C. V 1 V 2 = 1 7
D. V 1 V 2 = 3 7
Cho khối hộp ABCD.A'B'C'D' Gọi M là trung điểm của cạnh AB. Mặt phẳng (MB'D') chia khối hộp thành hai phần. Tính tỉ số thể tích hai phần đó.
A. 5 12
B. 7 17
C. 7 24
D. 5 17