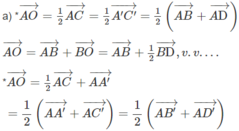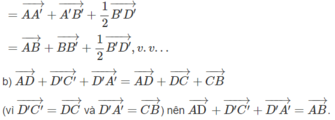Các câu hỏi tương tự
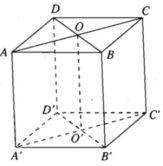
Cho hình lập phương ABCD.ABCD có cạnh bằng a . Gọi O và O lần lượt là tâm các hình vuông. Gọi M và N lần lượt là trung điểm của các cạnh B C và CD. Tính thể tích khối tứ diện OOMN
Đọc tiếp
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a . Gọi O và O' lần lượt là tâm các hình vuông. Gọi M và N lần lượt là trung điểm của các cạnh B' C' và CD. Tính thể tích khối tứ diện OO'MN
![]()
Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng a. Gọi O là tâm hình vuông ABCD và điểm S sao cho Tính độ dài đoạn OS theo a.
Đọc tiếp
Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng a. Gọi O là tâm hình vuông ABCD và điểm S sao cho ![]() Tính độ dài đoạn OS theo a.
Tính độ dài đoạn OS theo a.
![]()
![]()
![]()
![]()
Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng a. Gọi O là tâm hình vuông ABCD và điểm S thỏa mãn
O
S
→
O
A
→
+
O
B
→
+
O
C
→
+
O
D
→...
Đọc tiếp
Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng a. Gọi O là tâm hình vuông ABCD và điểm S thỏa mãn O S → = O A → + O B → + O C → + O D → + O A ' → + O B ' → + O C ' → + O D ' → . Tính độ dài đoạn OS theo a
A. OS=6a.
B. OS=4a.
C. OS=a.
D. OS=2a.
Trong mặt phẳng Oxy cho các điểm A(-3;2), B(-4;5) và C(-1;3).a. Chứng minh rằng các điểm A’(2;3), B’(5;4) và C’(3;1) theo thứ tự là ảnh của A, B và C qua phép quay tâm O góc
–
90
o
.b. Gọi tam giác
A
1
B
1
C
1
là ảnh của tam giác ABC qua phép dời hình có được bằng cách thực hiện liên tiếp phép quay tâm O góc
–...
Đọc tiếp
Trong mặt phẳng Oxy cho các điểm A(-3;2), B(-4;5) và C(-1;3).
a. Chứng minh rằng các điểm A’(2;3), B’(5;4) và C’(3;1) theo thứ tự là ảnh của A, B và C qua phép quay tâm O góc – 90 o .
b. Gọi tam giác A 1 B 1 C 1 là ảnh của tam giác ABC qua phép dời hình có được bằng cách thực hiện liên tiếp phép quay tâm O góc – 90 o và phép đối xứng qua trục Ox. Tìm tọa độ các đỉnh của tam giác A 1 B 1 C 1 .
Chỉ cần đáp án thôi ạ
Cho hình lập phương ABCD.EFGH. Có bao nhiêu vecto bằng vecto AB có điểm đầu và điểm cuối là các đỉnh của hình lập phương đã cho?
A. 3
B. 1
C. 6.
D. 7
Cho điểm A cố định trên đường tròn (O) và một điểm C di động trên đường tròn đó. Dựng hình vuông ABCD (thứ tự các đỉnh theo chiều dương). Khi đó quỹ tích điểm D là ảnh của đường tròn (O) qua phép biến hình F có được bằng cách thực hiện liên tiếp:
Đọc tiếp
Cho điểm A cố định trên đường tròn (O) và một điểm C di động trên đường tròn đó. Dựng hình vuông ABCD (thứ tự các đỉnh theo chiều dương). Khi đó quỹ tích điểm D là ảnh của đường tròn (O) qua phép biến hình F có được bằng cách thực hiện liên tiếp:
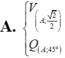
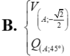
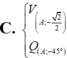
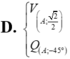
Cho hình chóp tứ giác đều S.ABCD có các cạnh bên và các cạnh đáy đều bằng a. Gọi O là tâm của hình vuông ABCD.
a) Tính độ dài đoạn SO.
b) Gọi M là trung điểm của đoạn SC. Chứng minh hai mặt phẳng (MBD) và (SAC) vuông góc với nhau.
c) Tính độ dài đoạn OM và tính góc giữa hai mặt phẳng (MBD) và (ABCD).
Cho hình vuông ABCD (các đỉnh hình vuông ghi theo chiều ngươ chiều kim đồng hồ) có tâm O. Phép quay tâm O với góc quay nào dưới đây biến điểm A thành điểm C ? A. 90 B.45 C. -90 D.180
Cho hình thang ABCD có AB // CD và AB 2a, BC CD DA a. Đường thẳng d vuông góc với mặt phẳng (ABCD) tại A. Gọi S là một điểm duy nhất thay đổi trên d. (P) là một mặt phẳng qua A vuông góc với SB tại I và cắt SC, SD lần lượt tại J, K.a) Chứng minh tứ giác BCJI, AIJK là các tứ giác nội tiếp.b) Gọi O là trung điểm của AB, O là tâm đường tròn ngoại tiếp tứ giác BCJI. Chứng minh rằng OO ⊥ (SBC).c) Chứng minh rằng khi S thay đổi trên d thì JK luôn luôn đi qua một điểm cố định.d) Tìm một điểm cách đ...
Đọc tiếp
Cho hình thang ABCD có AB // CD và AB = 2a, BC = CD = DA = a. Đường thẳng d vuông góc với mặt phẳng (ABCD) tại A. Gọi S là một điểm duy nhất thay đổi trên d. (P) là một mặt phẳng qua A vuông góc với SB tại I và cắt SC, SD lần lượt tại J, K.
a) Chứng minh tứ giác BCJI, AIJK là các tứ giác nội tiếp.
b) Gọi O là trung điểm của AB, O' là tâm đường tròn ngoại tiếp tứ giác BCJI. Chứng minh rằng OO' ⊥ (SBC).
c) Chứng minh rằng khi S thay đổi trên d thì JK luôn luôn đi qua một điểm cố định.
d) Tìm một điểm cách đều các điểm A, B, C, D, I, J, K và tìm khoảng cách đó.
e) Gọi M là giao điểm của JK và (ABCD). Chứng minh rằng AM là tiếp tuyến của đường tròn ngoại tiếp tam giác ABC.
f) Khi S thay đổi trên d, các điểm I, J, K lần lượt chạy trên đường nào.