Các câu hỏi tương tự
Cho bốn điểm A(1; 0; 0), B(0; 1; 0), C(0; 0; 1), D(-2; 1; -1) Tìm góc giữa hai đường thẳng AB và CD
Cho hàm số y 2x3-3x2+1 có đồ thị và đường thẳng d: yx-1. Giao điểm của (C) và d lần lượt là A( 1; 0); B và C. Khi đó khoảng cách giữa B và C là A. BC
30
2
B. BC
34
2
C. BC
3
2
2
D. BC
14
2
Đọc tiếp
Cho hàm số y= 2x3-3x2+1 có đồ thị và đường thẳng d: y=x-1. Giao điểm của (C) và d lần lượt là A( 1; 0); B và C. Khi đó khoảng cách giữa B và C là
A. BC= 30 2
B. BC= 34 2
C. BC= 3 2 2
D. BC= 14 2
Cho A(1; -2; 1), B(0; -1; 3),
C
-
2
;
0
;
4
, D(0; 2; -2). Gọi (P) là mp chiếu A, B và (P) cách đều C, D. Biết C, D thuộc 2 phía của (P). Tìm một vectơ pháp tuyến của (P).
Đọc tiếp
Cho A(1; -2; 1), B(0; -1; 3), C - 2 ; 0 ; 4 , D(0; 2; -2). Gọi (P) là mp chiếu A, B và (P) cách đều C, D. Biết C, D thuộc 2 phía của (P). Tìm một vectơ pháp tuyến của (P).
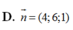
Cho hình lập phương ABCD.
A
1
B
1
C
1
D
1
có cạnh bằng 1. Gọi M, N, P lần lượt là trung điểm của các cạnh B
B
1
, CD.
A
1...
Đọc tiếp
Cho hình lập phương ABCD. A 1 B 1 C 1 D 1 có cạnh bằng 1. Gọi M, N, P lần lượt là trung điểm của các cạnh B B 1 , CD. A 1 D 1 . Tính khoảng cách và góc giữa hai đường thẳng MP và C 1 N.
Cho hình lăng trụ ngũ giác ABCD.A'B'C'D'. Gọi A'', B'', C'', D'', E'' lần lượt là trung điểm của các cạnh AA', BB', CC', DD', EE'. Tỉ số thể tích giữa khối lăng trụ ABCDE.A''B''C''D''E'' và khối lăng trụ ABCDE.A'B'C'D' bằng:
A. 1/2 B. 1/4
C. 1/8 D. 1/10.
câu 1 :cho hình lăng trụ đứng ABCD.A1B1C1D1 có đáy ABCD là hình thoi cạnh 4, góc BAD=60 độ, góc giữa (D1AC) và (ABCD)=60 độ. tính khoảng cách giữa 2 đường thẳng BD và AD1
câu 2: cho hệ tọa độ Oxy, biết đường thẳng d: 3x+4y+4=0 cắt đường tròn (C) có tâm là I(1;2) tại 2 điểm A,B sao cho AB=8. Đường tròn (C) có phương trình là gì??
CH 1.Trong không gian Oxyz ; Cho 3 điểm: A(-1; 1; 4) , B(1;- 1; 5) và C(1; 0; 3), toạ độ điểm D để ABCD là một hình bình hành là: A. D(-1; 2; 2) C. D(-1;-2 ; 2) D. D(1; -2; -2)CH 2.Trong không gian Oxyz cho 2 điểm A (1;–2;2) và B (– 2:0;1). Toạ độ điềm C nằm trên trục Oz để A ABC cân tại C là : A. C(0;0;2) C. C(0;–1;0) B. D(1; 2; -2) В. С(0,:0,-2) D. C( ;0;0)CH 3. Trong không gian Oxyz cho 2 vectơ a (1; 2; 2) và (1; 2; -2); khi đó : ¿(i+6) có giá trị bằng : С. 4 A. 10 В. 18 D. 8CH 4.Trong không...
Đọc tiếp
CH 1.Trong không gian Oxyz ; Cho 3 điểm: A(-1; 1; 4) , B(1;- 1; 5) và C(1; 0; 3), toạ độ điểm D để ABCD là một hình bình hành là: A. D(-1; 2; 2) C. D(-1;-2 ; 2) D. D(1; -2; -2)
CH 2.Trong không gian Oxyz cho 2 điểm A (1;–2;2) và B (– 2:0;1). Toạ độ điềm C nằm trên trục Oz để A ABC cân tại C là : A. C(0;0;2) C. C(0;–1;0) B. D(1; 2; -2) В. С(0,:0,-2) D. C( ;0;0)
CH 3. Trong không gian Oxyz cho 2 vectơ a =(1; 2; 2) và (1; 2; -2); khi đó : ¿(i+6) có giá trị bằng : С. 4 A. 10 В. 18 D. 8
CH 4.Trong không gian Oxyz cho 2 vecto a= (3; 1; 2) và b= (2; 0; -1); khi đó vectơ 2a-b có độ dài bằng : А. 3/5 В. 29 С. M D. S/5
CH 5. Cho hình bình hành ABCD với A (-1;0;2), B(3;4;0) D (5;2;6). Tìm khẳng định sai. A. Tâm của hình bình hành có tọa độ là (4;3;3) B. Vecto AB có tọa độ là (4;-4;-2) C. Tọa độ của điểm C là (9;6;4) D. Trọng tâm tam giác ABD có tọa độ là (3;2;2)
Cho bốn điểm A(1; 0; 0), B(0; 1; 0), C(0; 0; 1), D(-2; 1; -1) Chứng minh A, B, C, D là bốn đỉnh của một tứ diện.
Cho bốn điểm A(1; 0; 0), B(0; 1; 0), C(0; 0; 1), D(-2; 1; -1) Tính độ dại đường cao của hình chóp A.BCD
Cho hàm số
y
a
x
4
+
b
x
2
+
c
có đồ thị (C) biết rằng (C) đi qua điểm A(-1;0) tiếp tuyến d tại A của (C) cắt (C) tại hai điểm có hoành độ lần lượt là 0 và 2, diện tích hình phẳng giới hạn bởi d, đồ thị (C) và hai đường thẳng x0; x2 có diện tích bằng 28/5 (phần gạch chéo trong hình vẽ). Diện tích hình phẳng giới hạn bởi d, đồ thị (C) và...
Đọc tiếp
Cho hàm số y = a x 4 + b x 2 + c có đồ thị (C) biết rằng (C) đi qua điểm A(-1;0) tiếp tuyến d tại A của (C) cắt (C) tại hai điểm có hoành độ lần lượt là 0 và 2, diện tích hình phẳng giới hạn bởi d, đồ thị (C) và hai đường thẳng x=0; x=2 có diện tích bằng 28/5 (phần gạch chéo trong hình vẽ). Diện tích hình phẳng giới hạn bởi d, đồ thị (C) và hai đường thẳng x=-1; x = 0 có diện tích bằng:
A. 2/5
B. 1/9
C. 2/9
D. 1/5