Chọn B.
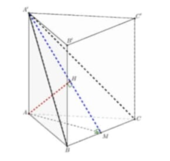
Gọi M là trung điểm của BC, AM= a 3 2 , BC ⊥ (A'AM)
Kẻ AH ⊥ A'M, suy ra AH ⊥ (A'BC) và AH=d(A,(A'BC))
Xét tam giác A'AM vuông tại A, ta có:
1 A H 2 = 1 A A ' 2 + 1 A M 2 ⇒ A H = a 21 7
Vậy d(A,(A'BC))= a 21 7
Chọn B.

Gọi M là trung điểm của BC, AM= a 3 2 , BC ⊥ (A'AM)
Kẻ AH ⊥ A'M, suy ra AH ⊥ (A'BC) và AH=d(A,(A'BC))
Xét tam giác A'AM vuông tại A, ta có:
1 A H 2 = 1 A A ' 2 + 1 A M 2 ⇒ A H = a 21 7
Vậy d(A,(A'BC))= a 21 7
Cho hình lăng trụ tam giác đều ABC.A'B'C' có tất cả các cạnh bằng a. Khoảng cách từ A đến mặt phẳng (A'BC) bằng
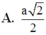
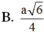
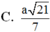
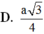
Cho hình lăng trụ tam giác đều ABC.A'B'C' có tất cả các cạnh bằng a. Khoảng cách từ A đến mặt phẳng (A'BC) bằng:
A. a 2 2
B. a 3 4
C. a 21 7
D. a 6 4
Cho hình lăng trụ đứng tam giác đều ABC.A'B'C' có cạnh đáy bằng 2a. Mặt bên có diện tích bằng 4 a 2 . Tính khoảng cách từ A đến mặt phẳng(A'BC) theo a.
A. 2 a 5 5
B. 3 a 5 5
C. 2 a 13 13
D. 2 a 21 7
Cho hình lăng trụ đứng ABC.A'B'C', biết đáy ABC là tam giác đều cạnh a. Khoảng cách từ tâm O của tam giác ABC đến mặt phẳng (A'BC) bằng a 6 . Thể tích khối lăng trụ ABC.A'B'C' là:
A. 3 a 3 12 16
B. 3 a 3 12 8
C. 3 a 3 2 28
D. 3 a 3 2 4
Cho lăng trụ tam giác ABC.A'B'C' có khoảng cách từ A đến mặt phẳng (A'BC) bằng 6a. Khoảng cách từ trung điểm M của cạnh B'C' đến mặt phẳng (A'BC) bằng
![]()
![]()
![]()
![]()
Cho khối lăng trụ tam giác đều ABC. A'B'C' có cạnh đáy là a và khoảng cách từ A đến mặt phẳng (A'BC) bằng a/2. Thể tích của khối lăng trụ bằng:
A. 3 2 a 3 12
B. 2 a 3 16
C. 3 a 3 2 16
D. 3 a 3 2 48
Cho hình lăng trụ tam giác đều
ABC.A'B'C' có cạnh đáy bằng a, góc
giữa mặt phẳng (A'BC ) và mặt phẳng
( ABC ) bằng 45o. Thể tích của khối
lăng trụ ABC.A'B'C' bằng
![]()
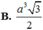
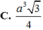
![]()
Cho hình lăng trụ đứng ABC. A'B'C' có đáy ABC là tam giác đều cạnh a. Khoảng cách từ tâm O của tam giác ABC đến mặt phẳng (A'BC) bằng a 6 . Thể tích khối lăng trụ bằng
A. 3 a 3 2 4
B. 3 a 3 2 8
C. 3 a 3 2 28
D. 3 a 3 2 16
Lăng trụ tam giác đều ABC.A'B'C' có tất cả các cạnh bằng a. Tính khoảng cách h từ C' đến (A'B'C').
A. h = a 3 4
B. h = a 3
C. h = a 3 7
D. h = a 2 4