Các câu hỏi tương tự
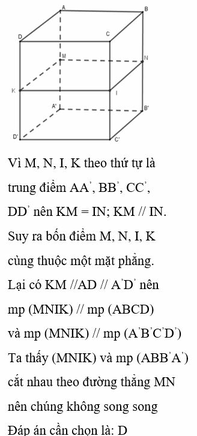
Cho hình hộp chữ nhật ABCD. A’B’C’D’. Gọi M, N, I, K theo thứ tự là trung điểm AA’, BB’, CC’, DD’. Hãy chọn câu sai A. MK // IN B. mp (MNIK) // mp (ABCD) C. mp (MNIK) // mp (ABB’A’) D. mp (ABCD) // mp (A’B’C’D’)
Đọc tiếp
Cho hình hộp chữ nhật ABCD. A’B’C’D’. Gọi M, N, I, K theo thứ tự là trung điểm AA’, BB’, CC’, DD’. Hãy chọn câu sai
A. MK // IN
B. mp (MNIK) // mp (ABCD)
C. mp (MNIK) // mp (ABB’A’)
D. mp (ABCD) // mp (A’B’C’D’)
Cho hình hộp chữ nhật
A
B
C
D
.
A
B
C
D
.
Chứng minh rằng :a) BDD’B’ là hình chữ nhật
b
)
B
B
’
⊥
m
p
(
A
B
C
D
)
c
)
m
p
(
A
B
B
’
A
’
)
⊥...
Đọc tiếp
Cho hình hộp chữ nhật A B C D . A ' B ' C ' D ' . Chứng minh rằng :
a) BDD’B’ là hình chữ nhật
b ) B B ’ ⊥ m p ( A B C D ) c ) m p ( A B B ’ A ’ ) ⊥ m p ( A B C D )
Cho hình hộp chữ nhật ABCD. A’B’C’D’ có O và O’ lần lượt là tâm ABCD; A’B’C’D’. Hai mp (ACC’A’) và mp (BDD’B’) cắt nhau theo đường nào? A. OO’ B. CC’ C. AD D. AO
Đọc tiếp
Cho hình hộp chữ nhật ABCD. A’B’C’D’ có O và O’ lần lượt là tâm ABCD; A’B’C’D’. Hai mp (ACC’A’) và mp (BDD’B’) cắt nhau theo đường nào?
A. OO’
B. CC’
C. AD
D. AO
Cho hình hộp chữ nhật
A
B
C
D
.
A
B
C
D
.
Chứng minh rằng:
a
)
B
D
/
/
B
’
D
’
b
)
B
B
’
/
/
m
p
(
C
C
’...
Đọc tiếp
Cho hình hộp chữ nhật A B C D . A ' B ' C ' D ' . Chứng minh rằng:
a ) B D / / B ’ D ’
b ) B B ’ / / m p ( C C ’ D ’ D ) , B ’ D ’ / / m p ( A B C D )
c ) m p ( A B B ’ A ’ ) / / m p ( D C C ’ D ’ )
Cho hình hộp chữ nhật
A
B
C
D
.
A
B
C
D
.
Chứng minh rằng:
a
)
B
D
/
/
B
’
D
’
b
)
B
B
’
/
/
m
p
(
C
C
’...
Đọc tiếp
Cho hình hộp chữ nhật A B C D . A ' B ' C ' D ' . Chứng minh rằng:
a ) B D / / B ’ D ’
b ) B B ’ / / m p ( C C ’ D ’ D ) , B ’ D ’ / / m p ( A B C D )
c ) m p ( A B B ’ A ’ ) / / m p ( D C C ’ D ’ )
Bài 1: cho hình thang vuông abcd, BC90° và AD không song song với BC. Trên đường thẳng vuông góc với mp(ABCD) tại B, lấy điểm S và nối S với A,C,D.a) Chứng minh AB⊥mp(SBC)b) Chứng minh mp(SBC) ⊥mp(ABCD).c) Tìm giao tuyến của 2 mặt phẳng (SBC) và (SAD).Bài 2 : Cho hình hộp chữ nhật ABCD.EFGH.a) Đường thẳng BF vuông góc với những mặt phẳng nào?b) CHứng minh mp(AEHD) ⊥mp(CGHD).c) Gọi M, P theo thứ tự là trung điểm của AE,CG. Chứng minh MP//AC.d) Gọi N, Q theo...
Đọc tiếp
Bài 1: cho hình thang vuông abcd, B=C=90° và AD không song song với BC. Trên đường thẳng vuông góc với mp(ABCD) tại B, lấy điểm S và nối S với A,C,D.
a) Chứng minh AB⊥mp(SBC)
b) Chứng minh mp(SBC) ⊥mp(ABCD).
c) Tìm giao tuyến của 2 mặt phẳng (SBC) và (SAD).
Bài 2 : Cho hình hộp chữ nhật ABCD.EFGH.
a) Đường thẳng BF vuông góc với những mặt phẳng nào?
b) CHứng minh mp(AEHD) ⊥mp(CGHD).
c) Gọi M, P theo thứ tự là trung điểm của AE,CG. Chứng minh MP//AC.
d) Gọi N, Q theo thứ tự là trung điểm của BF,DH. Chứng tỏ M,N,P,Q cùng nằm trên 1 mặt phẳng và mp(MNPQ) song song với những mặt phẳng nào?
cho tứ giác ABCD. Gọi M, N, P, Q, R, S lần lượt là trung điểm của AB, BC, CD, DA, AC, BD.a, Chứng minh các đường thẳng MP, NQ, RS đồng quy tại I.b, Chứng minh đường thẳng AI đi qua trọng tâm A của tam giác BCD và IA3IA.c, Gọi B, C, D theo thứ tự là trọng tâm của các tam giác ACD, ABD, ABC. Chứng minh rằng các đường thẳng AA, BB cắt nhau tại một điểm và điểm này chia các đoạn AA, BB, CC, DD theo cùng một tỉ số.
Đọc tiếp
cho tứ giác ABCD. Gọi M, N, P, Q, R, S lần lượt là trung điểm của AB, BC, CD, DA, AC, BD.
a, Chứng minh các đường thẳng MP, NQ, RS đồng quy tại I.
b, Chứng minh đường thẳng AI đi qua trọng tâm A' của tam giác BCD và IA=3IA'.
c, Gọi B', C', D' theo thứ tự là trọng tâm của các tam giác ACD, ABD, ABC. Chứng minh rằng các đường thẳng AA', BB' cắt nhau tại một điểm và điểm này chia các đoạn AA', BB', CC', DD' theo cùng một tỉ số.
Cho tứ giác ABCD. Gọi E, F theo thứ tự là trung điểm của AB và CD; M, N, P, Q lầ lượt là trung điểm của các đoạn thẳng AF, CE, BF và DE. Gọi I là giao điểm của MP và EF. Chứng minh rằng:
a) I là trung điểm của MP
b) MNPQ là hình bình hành
Hình thang ABCD (AB//CD) có M, N, P, Q thứ tự là trung điểm của AB, BC, CD, DA. Khẳng định nào sau đây đúngA. MP // BC B. MP // BC và MP C. NQ D. NQ //AB và NQ
Đọc tiếp
Hình thang ABCD (AB//CD) có M, N, P, Q thứ tự là trung điểm của AB, BC, CD, DA. Khẳng định nào sau đây đúng
A. MP // BC B. MP // BC và MP=
C. NQ = D. NQ //AB và NQ =