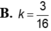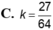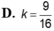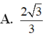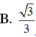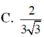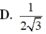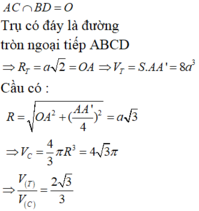Các câu hỏi tương tự
Cho hình hộp
A
B
C
D
.
A
B
C
D
có
A
B...
Đọc tiếp
Cho hình hộp A B C D . A ' B ' C ' D ' có A B = A D = 2 a , A A ' = 4 a Lấy M, N, P, Q lần lượt là trung điểm của A A ' , B B ' , C C ' , D D ' Biết hình hộp chữ nhật A B C D . A ' B ' C ' D ' nội tiếp khối trụ (T) và lăng trụ A B C D . M N P Q nội tiếp mặt cầu (C) Tỉ số thể tích V ( T ) V ( C ) giữa khối trụ và khối cầu là:
A. 2 3 3
B. 3 3
C. 2 3 3
D. 1 3 2
Cho hình hộp
A
B
C
D
.
A
B
C
D
có
A
B
A
D
2
a
,...
Đọc tiếp
Cho hình hộp A B C D . A ' B ' C ' D ' có A B = A D = 2 a , A A ' = 4 a . Lấy M, N, P, Q lần lượt là trung điểm của AA’, BB’,CC, DD’. Biết hình hộp chữ nhật A B C D . A ' B ' C ' D ' nội tiếp khối trụ (T) và lăng trụ ABCD.MNPQ nội tiếp mặt cầu (C). Tỉ số thể tích V ( T ) V ( C ) giữa khối cầu và khối trụ là
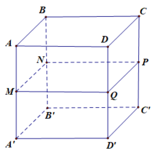
A. 2 3 3
B. 3 3
C. 2 3 3
D. 1 3 2
Cho hình hộp ABCD.ABCD có AB AD 2a, AA 4a . Lấy M, N, P, Q lần lượt là trung điểm của AA’, BB’, CC’, DD’. Biết hình hộp chữ nhật ABCD.ABCD nội tiếp khối trụ (T) và lăng trụ ABCD.MNPQ nội tiếp mặt cầu (C). Tỉ số thể tích
V
T
V
C
giữa khối cầu và khối trụ là.
Đọc tiếp
Cho hình hộp ABCD.A'B'C'D' có AB = AD = 2a, AA' = 4a . Lấy M, N, P, Q lần lượt là trung điểm của AA’, BB’, CC’, DD’. Biết hình hộp chữ nhật ABCD.A'B'C'D' nội tiếp khối trụ (T) và lăng trụ ABCD.MNPQ nội tiếp mặt cầu (C). Tỉ số thể tích V T V C giữa khối cầu và khối trụ là.
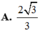
![]()
![]()
![]()
Cho hình lăng trụ ngũ giác ABCD.A'B'C'D'. Gọi A'', B'', C'', D'', E'' lần lượt là trung điểm của các cạnh AA', BB', CC', DD', EE'. Tỉ số thể tích giữa khối lăng trụ ABCDE.A''B''C''D''E'' và khối lăng trụ ABCDE.A'B'C'D' bằng:
A. 1/2 B. 1/4
C. 1/8 D. 1/10.
Cho hình hộp chữ nhật ABCD.ABCD có ABa, AD2a, AA3a. Thể tích khối cầu ngoại tiếp hình hộp chữ nhật ABCD.ABCD là
Đọc tiếp
Cho hình hộp chữ nhật ABCD.A'B'C'D' có AB=a, AD=2a, AA'=3a. Thể tích khối cầu ngoại tiếp hình hộp chữ nhật ABCD.A'B'C'D' là
![]()
![]()
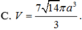
![]()
Cho hình lăng trụ đứng ABCD.ABCD có đáy là hình thoi, biết
A
A
4
a
,
A
C
2
a
,
B
D
a
. Thể tích V của khối lăng trụ là.
Đọc tiếp
Cho hình lăng trụ đứng ABCD.A'B'C'D' có đáy là hình thoi, biết A A ' = 4 a , A C = 2 a , B D = a . Thể tích V của khối lăng trụ là.
![]()
![]()
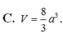
![]()
Cho lăng trụ đứng ABCD.ABCD có đáy ABCD là hình thang, AB AD a, CD 2a. Đường thẳng A’C tạo với mặt phẳng (ABCD) một góc bằng 60o. Biết hình lăng trụ nội tiếp một hình trụ. Tính thể tích khối trụ ngoại tiếp lăng trụ theo a ta được: A.
3
πa
3
B.
πa
3
C.
4
πa
3...
Đọc tiếp
Cho lăng trụ đứng ABCD.A'B'C'D có đáy ABCD là hình thang, AB = AD = a, CD = 2a. Đường thẳng A’C tạo với mặt phẳng (ABCD) một góc bằng 60o. Biết hình lăng trụ nội tiếp một hình trụ. Tính thể tích khối trụ ngoại tiếp lăng trụ theo a ta được:
A. 3 πa 3
B. πa 3
C. 4 πa 3 3
D. πa 3 3
Cho khối lăng trụ tam giác ABC. ABC. Gọi M, N lần lượt là trung điểm của BB và CC. Mặt phẳng (AMN) chia khối lăng trụ thành hai phần. Gọi V₁ là thể tích của khối đa diện chứa đỉnh B và V₂ là thể tích khối đa diện còn lại. Tính tỉ số V₁/V₂. A.
V
1
V
2
7
2
B.
V
1...
Đọc tiếp
Cho khối lăng trụ tam giác ABC. A'B'C'. Gọi M, N lần lượt là trung điểm của BB' và CC'. Mặt phẳng (AMN) chia khối lăng trụ thành hai phần. Gọi V₁ là thể tích của khối đa diện chứa đỉnh B' và V₂ là thể tích khối đa diện còn lại. Tính tỉ số V₁/V₂.
A. V 1 V 2 = 7 2
B. V 1 V 2 = 2
C. V 1 V 2 = 1 3
D. V 1 V 2 = 5 2
Một khối trụ tròn nội tiếp trong một mặt cầu (Hình vẽ), biết chiều cao hình trụ bằng bán kính mặt cầu, tính tỉ số
k
V
1
V
2
với
V
1
,
V
2
lần lượt là thể tích khối trụ và mặt cầu
Đọc tiếp
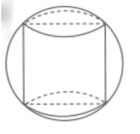
Một khối trụ tròn nội tiếp trong một mặt cầu (Hình vẽ), biết chiều cao hình trụ bằng bán kính mặt cầu, tính tỉ số k = V 1 V 2 với V 1 , V 2 lần lượt là thể tích khối trụ và mặt cầu
![]()