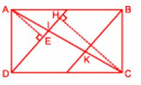
Ta có : dt (ABC) = 2 x dt (AMD) (vì AB = 2 x AM và AD = BC) ; dt (DCM) = dt (ABC) (vì AB = DC và c.cao cùng bằng BC)
Suy ra dt (DCM) = 2 x dt (AMD). Gọi CH và AE lần lượt là chiều cao của tam giác DCM và DAM xuống đáy DM, khi đó CH = 2 x AE. Nhưng CH và AE lần lượt là chiều cao của tam giác ICM và IAM có chung cạnh đáy IM. Vậy dt (ICM) = 2 x dt (IAM). Mà tam giác IAM và ICM chung chiều cao từ M, do đó IC = 2 x AI, suy ra AC = 3 x AI hay AI = 1/3 AC.
Làm tương tự với các cặp tam giác ABN và CBN ; KCN và KAN ta có KC = 1/3 AC. Vậy AI = KC = 1/3 AC, suy ra IK = 1/3 AC.
Do đó AI = IK = KC.