- Phép đối xứng qua tâm I biến ΔAEI thành ΔCFI
- Phép đối xứng qua trục d biến ΔCFI thành ΔFCH
- Phép đối xứng qua tâm I biến ΔAEI thành ΔCFI
- Phép đối xứng qua trục d biến ΔCFI thành ΔFCH
Cho hình thoi ABCD tâm O. Gọi E, F, M, N lần lượt là trung điểm các cạnh AB, CD, BC, AD. P là phép đồng dạng biến tam giác OCF thành tam giác CAB. Tìm mệnh đề sai trong các mệnh đề sau:
A. P hợp thành bởi phép đối xứng tâm O và phép vị tự tâm A tỉ số k = 2
B. P hợp thành bởi phép đối xứng trục AC và phép vị tự tâm C tỉ số k = 2
C. P hợp thành bởi phép vị tự tâm C tỉ số k = 2 và phép đối xứng tâm O
D. P hợp thành bởi phép đối xứng trục BD và phép vị tự tâm O tỉ số k = -1
Cho hình chữ nhật ABCD tâm I với E, F, G, H lần lượt là trung điểm của DA, AB, BC và CD như hình vẽ, phép biến hình biến hình (1) thành hình (3) là thực hiện liên tiếp hai phép dời hình nào sau đây.

A. Phép đối xứng tâm I và phép đối xứng trục IB.
B. Phép đối xứng tâm I và phép quay tâm I góc quay 90 o .
C. Phép đối xứng trục EI và phép tịnh tiến theo D I → .
D. Phép tịnh tiến theo A I → và phép đối xứng tâm I.
Cho hình chữ nhật ABCD tâm I. Gọi E, F, G, H lần lượt là trung điểm của AB, CD, CI, FC. Phép đồng dạng hợp thành bởi phép vị tự tâm C tỉ số k = 2 và phép đối xứng tâm I biến tứ giác IGHF thành:
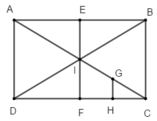
A. AIFD
B. BCFI
C. CIEB
D. DIEA
Cho hình chữ nhật ABCD tâm I. Gọi E, F, G, H lần lượt là trung điểm của AB, CD, CI, FC. Phép đồng dạng hợp thành bởi phép vị tự tâm C tỉ số k=2 và phép đối xứng tâm I biến tứ giác IGHF thành
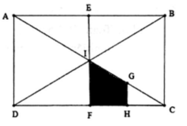
A. AIFD
B. BCFI
C. CIEB
D. DIEA
Cho tam giác ABC có A’, B’, C’ theo thứ tự là trung điểm của các cạnh BC, CA, AB. Tìm một phép vị tự biến tam giác ABC thành tam giác A’B’C’ (h.1.56).
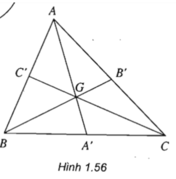
Cho hình chữ nhật ABCD. Gọi O là tâm đối xứng của nó. Gọi I, F, J, E lần lượt là trung điểm của các cạnh AB, BC, CD, DA. Tìm ảnh của tam giác AEO qua phép đồng dạng có được từ việc thực hiện liên tiếp phép đối xứng qua đường thẳng IJ và phép vị tự tâm B, tỉ số 2.
Số phát biểuđúng là:
a) Phép tịnh tiến biến đường thẳng thành đường thẳng song song hoặc trùng với nó
b) Phép biến hình biến đường tròn thành đường tròn có bán kính bằng nó là phép tịnh tiến
c) Phép tịnh tiến biến tứ giác thành tứ giác bằng nó
d) Phép tịnh tiến biến đường tròn thành chính nó
e) Phép đồng nhất biến mọi hình thành chính nó
f) Phép dời hình là 1 phép biến hình không làm thay đồi khoảng cách giữa hai điểm bất kì
g) Phép chiếu lên đường thẳng không là phép dời hình
h) Với bất kì 2 điểm A, B và ảnh A’, B’ của chúng qua 1 phép dời hình, ta luôn có A’B = AB’.
i) Nếu phép dời hình F biến tam giác ABC thành tam giác A’B’C’ thì trọng tâm tam giác ABC biến thành trọng tâm tam giác A’B’C’.
k) Phép tịnh tiến theo vectơ là phép đồng nhất.
l) Nếu phép dời hình biến điểm A thành điểm B ( B ≠ A ) thì nó cũng biến điểm B thành A
m) Nếu phép dời hình biến điểm A thành điểm B và biến điểm B thành điểm C thì AB = BC
A.5
B.6
C.7
D.8
Cho hình vuông ABCD tâm I. gọi E, F, G, H lần lượt là trung điểm của các cạnh DA, AB, BC, CD. Phép đối xứng trục AC biến:
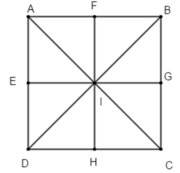
A. ∆IED thành ∆IGC
B. ∆IFB thành ∆IGB
C. ∆IBG thành ∆IDH
D. ∆IGC thành ∆IFA
Cho tam giác ABC có trọng tâm G, trực tâm H, tâm đường tròn ngoại tiếp O. gọi D, E, F lần lượt là trung điểm các cạnh BC, CA, AB.
Phép vị tự tâm G tỉ số -1/2 biến tam giác ABC thành
A. Tam giác GBC
B. Tam giác DEF
C. Tam giác AEF
D. Tam giác AFE