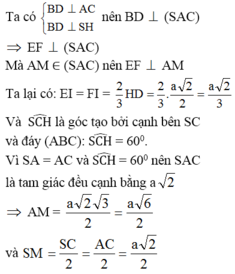

Điều này chứng tỏ SM là đường cao của hình chóp S.AEMF. Vậy thể tích của khối chóp S.AEMF là:
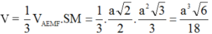

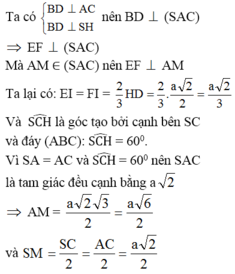

Điều này chứng tỏ SM là đường cao của hình chóp S.AEMF. Vậy thể tích của khối chóp S.AEMF là:
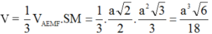
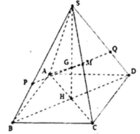
Cho hình chóp tứ giác đều S.ABCD, đáy là hình vuông cạnh a, cạnh bên tạo với đáy một góc 60 o . Gọi M là trung điểm của SC. Mặt phẳng đi qua AM và song song với BD, cắt SB tại P và cắt SD tại Q. Thể tích khối chóp S.AMNQ là V. Tỉ số 18 V a 3 là ?
A. 2
B. 6
C. 3
D. 1
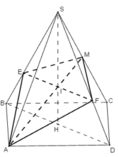
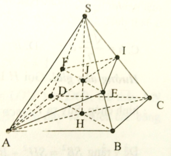
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a, cạnh bên bằng a 2 . Mặt phẳng (P) qua A và vuông góc với SC cắt SB, SC, SD lần lượt tại E, I, F. Tính tỉ số k giữa thể tích hình chóp S.AEIF và thể tích hình chóp S.ABCD.
A. k = 1 4
B. k = 1 3
C. k = 1 6
D. k = 2 9
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành, gọi M là trung điểm của cạnh bên SC. Mặt phẳng (P) qua AM và song song với BD lần lượt cắt các cạnh bên SB, SD tại N, Q. Đặt t = V S . A N M Q V S . A B C D . Tính t.
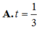
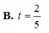
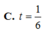
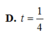
Cho hình chóp tứ giác đều S. ABCD, M là trung điểm của SC. Mặt phẳng (P) qua AM và song song với BD cắt SB, SD tại N, K. Tính tỉ số thể tích của khối S. ANMK và khối chóp S.ABCD.
A. 2 9
B. 1 3
C. 1 2
D. 3 5
Cho hình chóp đều S. ABCD có độ dài cạnh đáy bằng α . Gọi G là trọng tâm tam giác SAC . Mặt phẳng chứa AB và đi qua G cắt các cạnh SC, SD lần lượt tại M và N. Biết mặt bên của hình chóp tạo với đáy một góc bằng 60 ° . Thể tích khối chóp S.ABCD bằng
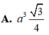
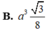

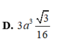
Cho hình chóp S.ABCD có đáy là hình vuông cạnh 2 2 , cạnh bên SA vuông góc với mặt phẳng đáy. Mặt phẳng α qua A và vuông góc với SC cắt cạnh SB, SC, SD lần lượt tại các điểm M, N, P. Thể tích V của khối cầu ngoại tiếp tứ diện CMNP là:
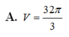
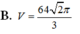
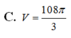
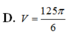
Cho hình chóp S.ABCD có đáy là hình vuông cạnh 2 2 , cạnh bên SA vuông góc với mặt phẳng đáy. Mặt phẳng ( α ) qua A và vuông góc với SC cắt cạnh SB, SC, SD lần lượt tại các điểm M, N, P. Thể tích V của khối cầu ngoại tiếp tứ diện CMNP bằng
![]()
![]()
![]()
![]()
Cho hình chóp S.ABCD có đáy là hình vuông cạnh 2 2 , cạnh bên SA vuông góc với mặt phẳng đáy và SA=3. Mặt phẳng α qua A và vuông góc với SC cắt cạnh SB, SC, SD lần lượt tại các điểm M, N, P. Thể tích V của khối cầu ngoại tiếp tứ diện CMNP
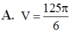
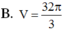
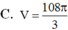
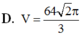
Cho hình chóp S.ABCD có đáy là hình vuông cạnh 2 2 cạnh bên SA vuông góc với mặt phẳng đáy và SA=3. Mặt phẳng α qua A và vuông góc với SC cắt cạnh SB, SC, SD lần lượt tại các điểm M, N, P. Thể tích V của khối cầu ngoại tiếp tứ diện CMNP
A. V = 125 π 6
B. V = 32 π 3
C. V = 108 π 3
D. V = 64 2 π 3