Question

Cho hình chóp tứ giác đều S.ABCD có cạnh bằng a, cạnh bên bằng 2a căn 2. Gọi M là trung điểm của SA. Góc giữa đường thẳng BM với mặt phẳng (ABCD) bằng bao nhiêu độ?

Answer 1

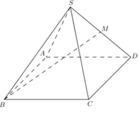
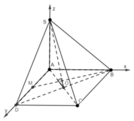
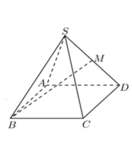
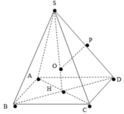
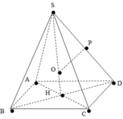
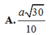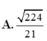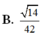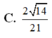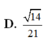Xét (SAO) Kẻ MH vuông góc vs AO ( với H là trung điểm AO)

Do M là trung điểm SA, H là trung điểm AO 

=> MH // SO, SO vuông đáy => MH vuông đáy

=> (BM;(ABCD)) = (BM;BH) = ^HBM 

Theo Pytago tam giác BAD vuông tại A => BD = \(\sqrt{2}a\)

=> BO = \(\dfrac{\sqrt{2}a}{2}\)

Theo Pytago tam giác SOB vuông tại O 

\(SO=\sqrt{8a^2-\dfrac{2}{4}a^2}=\dfrac{\sqrt{30}}{2}a\)

Do MH là đường trung bình \(MH=\dfrac{\sqrt{30}}{4}a\)

Xét tam giác SAB => cosSAB = \(\dfrac{\sqrt{2}}{8}\)

áp vào với tam giác AMB tính được BM, rồi bn xét tam giác MHB, dùng sin là ra góc cần tìm nhé