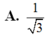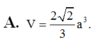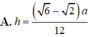Phương pháp:
+ Sử dụng định nghĩa để tìm góc giữa hai mặt phẳng (P) và (Q):
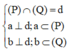
khi đó góc giữa (P) và (Q) chính là góc giữa hai đường thẳng a và b.
+ Sử dụng định lý hàm số cos trong tam giác để tính toán:
Cho tam giác ABC khi đó 
Cách giải:
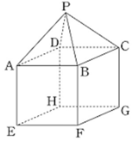
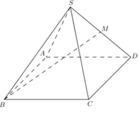
Hình chóp tứ giác đều S.ABCD có tất cả các cạnh đều bằng a, ta tìm góc giữa hai mặt phẳng (SAD) và (SBC).
Gọi M, N là trung điểm các cạnh AD và BC, khi đó SM ⊥ AD và SN ⊥ BC (do các tam giác SBC;SAD là các tam giác đều).
Vì BC//AD nên giao tuyến của hai mặt phẳng (SAD) và (SBC) là đường thẳng d qua S và song song AD, BC.
Vì SM
⊥
AD và SN
⊥
BC nên SM
⊥
d và SN
⊥
d mà 
góc giữa hai mặt phẳng (SAD) và (SBC) là góc MSN.
Mặt bên là các tam giác đều cạnh a nên 
Khi đó: 
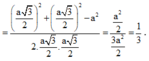
Chọn A
Chú ý khi giải:
Các em có thể tính SO theo tỉ số lượng giác và suy ra MSN = 2MSO
