Chọn A
Phương pháp:
Góc giữa đường thẳng và mặt phẳng là góc giữa đường thẳng và hình chiếu của nó trên mặt phẳng đó.
Cách giải

Chọn A
Phương pháp:
Góc giữa đường thẳng và mặt phẳng là góc giữa đường thẳng và hình chiếu của nó trên mặt phẳng đó.
Cách giải

Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a, chiều cao của chóp bằng a 3 2 . Góc giữa mặt bên và mặt đáy bằng
![]()
![]()
![]()
![]()
Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a, đường cao S H = a 3 3 . Tính góc giữa cạnh bên và mặt đáy của hình chóp
![]()
![]()
![]()
![]()
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a, góc giữa cạnh bên và mặt phẳng đáy bằng 600. Tính thể tích khối chóp S.ABCD.
A. a 3 6
B. a 3 6 3
C. a 3 6 6
D. a 3 6 2
Cho khối chóp tứ giác đều có cạnh đáy bằng a và thể tích là a 3 3 . Gọi t là tỉ số giữa độ dài cạnh bên và độ dài cạnh đáy của hình chóp. Tính t
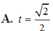
![]()
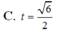
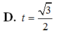
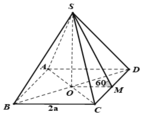
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng 2a, góc giữa mặt bên và mặt đáy bằng 60 ° . Tính theo a thể tích khối chóp S.ABCD
A. 4 a 3 3 3
B. a 3 3 3
C. 2 a 3 3 3
D. 2 a 3 6 3
Cho hình chóp tứ giác đều có tất cả các cạnh đều bằng a. Tính côsin của góc giữa mặt bên và mặt đáy.
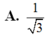
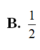
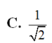
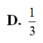
Cho hình chóp tứ giác đều có tất cả các cạnh bằng a. Côsin của góc giữa mặt bên và mặt đáy bằng:
A. 1 3
B. 1 3
C. 1 2
D. 1 2
Cho hình chóp tam giác đều S.ABC có độ dài cạnh đáy bằng a, góc hợp bởi cạnh bên và mặt đáy bằng 600. Tính thể tích khối chóp đã cho.
A. 3 a 3 12
B. 3 a 3 6
C. 3 a 3 3
D. 3 a 3 4
Cho hình chóp tứ giác đều SABCD , góc hợp bởi cạnh bên và mặt đáy bằng 60 độ, độ dài cạnh đáy bằng a . (α) qua A vuông góc với SC . Tính thiết diện tạo bởi (α) và mặt đáy