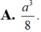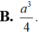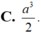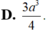Đáp án B
Dễ thấy AM + MN + NA đạt giá trị nhỏ nhất khi A, M, N, A thẳng hàng
Lại có S.ABC là hình chóp tam giác đều
=> ∆SAB = ∆SBC = ∆SAC (c.c.c)
=> AM + MN + NA min = a 2
Thị xã Từ Sơn xây dựng một ngọn tháp đèn lộng lẫy hình chóp tứ giác đều S.ABCD có cạnh bên SA = 12m và A S B ^ = 30 0 . Người ta cần mặc một đường dây điện từ điểm A đến trung điểm K của SA gồm 4 đoạn thẳng AE, EF, FH, HK như hình vẽ. Để tiết kiệm chi phí ngừơi ta cần thiết kế được chiều dài con đường từ A đến K là ngắn nhất. Tính tỉ số K = H F + H K E A + E F
A . k = 3 4
B . k = 1 2
C . k = 1 3
D . k = 2 3
Cho hình chóp tam giác đều S.ABC đỉnh S. Có độ dài cạnh đáy bằng a, cạnh bên bằng 2a. Gọi I là trung điểm của cạnh BC. Tính thể tích V của khối chóp S.ABI
A. V = a 3 11 12
B. V = a 3 11 24
C. V = a 3 11 8
D. V = a 3 11 6
Cho hình chóp S.ABC có đáy là tam giác đều cạnh a, SA = a 3 và vuông góc với mặt đáy. Gọi M là trung điểm cạnh SB (tham khảo hình vẽ bên). Côsin góc giữa hai đường thẳng AM và SC bằng
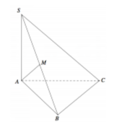
A. 5 16
B. 11 16
C. 5 8
D. 3 8
Cho hình chóp S.ABCD có cạnh bên SA = a (0 <a < 3 )và các cạnh còn lại đều bằng 1. Tính theo a thể tích V của khối chóp S.ABCD.
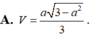
B. Đáp án khác.
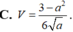
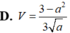
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B , AB =a, BC =a 3 Biết rằng SA vuông góc với mặt phẳng đáy và diện tích xung quanh của khối chóp S.ABC bằng 5 a 2 3 2 . Tính theo a khoảng cách d từ A đến mặt phẳng (SBC) gần với giá trị nào nhất sau đây ?
A. 0,72a
B. 0,9a
C. 0,8a
D. 1,12a
Cho hình chóp tam giác S.ABC có đáy ABC là tam giác đều cạnh a , SA=a và SA vuông góc với mặt phẳng (ABC). Gọi M và N lần lượt là hình chiếu vuông góc của A trên các đường thẳng SB và SC. Thể tích V của khối chóp A.BCMN bằng
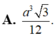
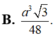
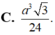
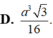
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, SA ⊥ (ABC) và SA = a/2.
M là trung điểm của BC. Khi đó góc giữa hai mặt phẳng (SAM) và (SBC) bằng:
A. 0 o
B. 30 o
C. 45 o
D. 60 o
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, AB = a, cạnh bên SA vuông góc với đáy và SA = a 2 . Gọi M là trung điểm của AB. Tính khoảng cách d giữa hai đường thẳng SM và BC
A . d = a 3 2
B . d = a 2 3
C . d = a 3 3
D . d = a 2
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, cạnh bên SA vuông góc với đáy, đường thẳng SC tạo với mặt phẳng đáy một góc 60 0 . Thể tích của khối chóp S.ABC bằng:
