Chọn C.
+) Do SA ⊥ (ABCD) ⇒ SA ⊥ BC nên câu A đúng.
+) Tam giác ABC vuông ở B nên AB ⊥ BC
- Lại có: SA ⊥ BC (vì SA ⊥ (ABCD))
→ Do đó: BC ⊥ (SAB) ⇒ AH ⊥ BC.
nên câu B đúng.
+) Theo trên ta có:
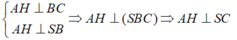
⇒ D đúng.
- Vậy câu C sai.
Chọn C.

+) Do SA ⊥ (ABCD) ⇒ SA ⊥ BC nên câu A đúng.
+) Tam giác ABC vuông ở B nên AB ⊥ BC
- Lại có: SA ⊥ BC (vì SA ⊥ (ABCD))
→ Do đó: BC ⊥ (SAB) ⇒ AH ⊥ BC.
nên câu B đúng.
+) Theo trên ta có:
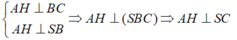
⇒ D đúng.
- Vậy câu C sai.
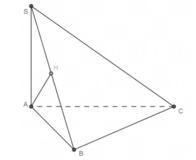
Cho hình chóp S.ABCD có SA ⊥ (ABCD) và ΔABC vuông ở B, AH là đường cao của ΔSAB. Khẳng định nào sau đây sai?
A. SA ⊥ BC
B. AH ⊥ BC
C. AH ⊥ AC
D. AH ⊥ SC
Cho hình chóp S.ABCD có SA ⊥ (ABCD) và ΔABC vuông ở B, AH là đường cao của ΔSAB. Khẳng định nào sau đây sai ?
A. SA ⊥ BC
B. AH ⊥ BC
C. AH ⊥ AC
D. AH ⊥ SC
Cho hình chóp S.ABCD có SA⊥(ABC) và tam giác ABC vuông ở B. Gọi AH là đường cao của tam giác SAB. Khẳng định nào sau đây sai?
A. SA⊥BC
B. AH⊥AC
C. AH⊥SC
D. AH⊥BC
Cho hình chóp S.ABCD có ABCD là hình chữ nhật có tâm O, AB a AC=3a. SA vuông góc với mp (ABCD); SC-5a. a) Chứng minh BC l S4F. b) Trong tam giác SAD kẻ AH vuông góc SD. Chứng minh AH _ (SCD) c Xác định và tinh góc giữa SO và (SCD).
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, S A ⊥ A B C và AH là đường cao của ∆ABC. Khẳng định nào sau đây sai?
A. S B ⊥ B C
B. A H ⊥ B C
C. S B ⊥ A C
D. A H ⊥ S C
Cho hình chóp S.ABC có SA ⊥ ( A B C ) và tam giác ABC vuông tại B, AH là đường cao của tam giác SAB . Khẳng định nào sau đây sai
![]()
![]()
![]()
![]()
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, SA ⊥ (ABC) và AH là đường cao của tam giác SAB. Khẳng định nào sau đây sai ?
![]()
![]()
![]()
![]()
cần giải gấp
Cho hình chóp S.ABCD có đáy là hình vuông cạnh = a, SA vuông góc (ABCD). Kẻ AH vuông góc SB, AK vuông góc SB.
a) BC vuông góc (SAB)
b) AH vuông góc SC
c) Gọi M là giao điểm của SC với (AHK). CM: HK vuông góc với AM
d) AH=?, HK=? biết SA=a\(\sqrt{3}\)
cho hình chóp S.ABCD; ABCD là hình vuông cạnh 2a; SA vuông góc với ABCD; SA = a căn 2. Kẻ AH vuôgn góc với Sb; AK vuông góc với SD. Chứng minh rằng: a) BC vuông góc SAB; b) BD vuông góc SAC; c) AH vuông góc SBC; d) SC vuông góc với AKH