Các câu hỏi tương tự
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a các mặt bên (SAB), (SAD) cùng vuông góc với mặt phẳng đáy, SAa; góc giữa đường thẳng SC và mặt phẳng (SAB) bằng a. Khi đó tan
α
nhận giá trị nào trong các giá trị sau:
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a các mặt bên (SAB), (SAD) cùng vuông góc với mặt phẳng đáy, SA=a; góc giữa đường thẳng SC và mặt phẳng (SAB) bằng a. Khi đó tan α nhận giá trị nào trong các giá trị sau:
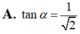
![]()
![]()
![]()
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 2a. Mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Gọi T là tâm mặt cầu ngoại tiếp hình chóp S. ABCD. Hỏi góc giữa hai đường thẳng TB và BD nằm trong khoảng nào dưới đây
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 2a. Mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Gọi T là tâm mặt cầu ngoại tiếp hình chóp S. ABCD. Hỏi góc giữa hai đường thẳng TB và BD nằm trong khoảng nào dưới đây


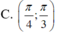
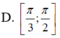
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, ABa;
A
D
a
3
2
. Mặt bên SAB là tam giác cân đỉnh S và nằm trong mặt phẳng vuông góc với mặt phẳng (ABCD). Biết
A
S
B
^
120
°
. Góc giữa hai mặt phẳng (SAD) và (SBC) bằng A. 60⁰. B. 30⁰. C. 45⁰. ...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB=a; A D = a 3 2 . Mặt bên SAB là tam giác cân đỉnh S và nằm trong mặt phẳng vuông góc với mặt phẳng (ABCD). Biết A S B ^ = 120 ° . Góc giữa hai mặt phẳng (SAD) và (SBC) bằng
A. 60⁰.
B. 30⁰.
C. 45⁰.
D. 90⁰.
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và D, ADDCa. Biết SAB là tam giác đều cạnh 2a và mặt phẳng (SAB) vuông góc với mặt phẳng (ABCD). Tính cosin của góc giữa hai mặt phẳng (SAB) và (SBC). A.
2
7
B.
2
6
C.
3
7
D.
5
7
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và D, AD=DC=a. Biết SAB là tam giác đều cạnh 2a và mặt phẳng (SAB) vuông góc với mặt phẳng (ABCD). Tính cosin của góc giữa hai mặt phẳng (SAB) và (SBC).
A. 2 7
B. 2 6
C. 3 7
D. 5 7
Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O cạnh a, SA vuông góc với đáy (ABCD) Góc giữa đường thẳng SC và mặt phẳng (SAB) bằng
α
với Tính góc giữa đường thẳng SO và mặt phẳng (ABCD) A.
60
o
B.
69
,
3
o
C.
90
o
D.
45
o
Đọc tiếp
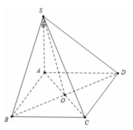
Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O cạnh a, SA vuông góc với đáy (ABCD) Góc giữa đường thẳng SC và mặt phẳng (SAB) bằng
α
với 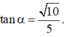 Tính góc giữa đường thẳng SO và mặt phẳng (ABCD)
Tính góc giữa đường thẳng SO và mặt phẳng (ABCD)
A. 60 o
B. 69 , 3 o
C. 90 o
D. 45 o
Cho hình chóp S.ABCD có đáy ABCD là hình vuông, hai mặt bên (SAB) và (SAD) vuông góc với mặt đáy. AH, AK lần lượt là đường cao của tam giác SAB, SAD. Mệnh đề nào sau đây là sai? A.
B
C
⊥
A
H
B.
S
A
⊥
A
C
C.
H
K
⊥
S
C
D.
A
K
⊥
B
D
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình vuông, hai mặt bên (SAB) và (SAD) vuông góc với mặt đáy. AH, AK lần lượt là đường cao của tam giác SAB, SAD. Mệnh đề nào sau đây là sai?
A. B C ⊥ A H
B. S A ⊥ A C
C. H K ⊥ S C
D. A K ⊥ B D
Cho hình chóp S.ABCD có đáy ABCD là hình vuông. Biết hai mặt phẳng (SAB) và (SAD) cùng vuông góc với mặt đáy. Hình chóp này có bao nhiêu mặt phẳng đối xứng
A. 4
B. 1
C. 0
D. 2
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Hai mặt bên (SAB) và (SAD) cùng vuông góc với mặt đáy. Biết góc giữa hai mặt phẳng (SCD) và (ABCD) bằng
45
0
. Gọi
V
1
;
V
2
lần lượt là thể tích khối chóp S.AHK và S.ACD với H, K lần lượt là trung đ...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Hai mặt bên (SAB) và (SAD) cùng vuông góc với mặt đáy. Biết góc giữa hai mặt phẳng (SCD) và (ABCD) bằng 45 0 . Gọi V 1 ; V 2 lần lượt là thể tích khối chóp S.AHK và S.ACD với H, K lần lượt là trung điểm cùa SC và SD. Tính độ dài đường cao của khối chóp S.ABCD và tỉ số k = V 1 V 2 .
A. h = a, k = 1 4
B. h =a , k = 1 6
C. h =2a, k = 1 8
D. h =2a, k = 1 3
Cho hình chóp S.ABCD có đáy ABCD là hình vuông, cạnh bên SA vuông góc với mặt phẳng đáy. Đường thẳng SD tạo với mặt phẳng (SAB) một góc 45⁰. Gọi I là trung điểm của cạnh CD. Góc giữa hai đường thẳng BI và SD bằng (Số đo góc được làm tròn đến hàng đơn vị). A. 39⁰. B. 42⁰. C. 51⁰. D. 48⁰.
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình vuông, cạnh bên SA vuông góc với mặt phẳng đáy. Đường thẳng SD tạo với mặt phẳng (SAB) một góc 45⁰. Gọi I là trung điểm của cạnh CD. Góc giữa hai đường thẳng BI và SD bằng (Số đo góc được làm tròn đến hàng đơn vị).
A. 39⁰.
B. 42⁰.
C. 51⁰.
D. 48⁰.



