Chọn A.
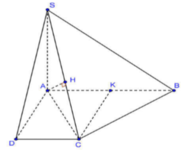
Gọi K là trung điểm AB => AK = KB = a
Dễ thấy tứ giác ADCK là hình vuông => CK = a
∆ ACB có trung tuyến CK = 1 2 AB => ∆ ACB vuông tại C.
Ta có: 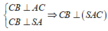
![]()
Trong (SAC) từ A hạ AH ⊥ SC tại H => AH ⊥ (SBC)
∆
SAC vuông tại A 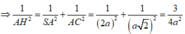
![]()
Chọn A.

Gọi K là trung điểm AB => AK = KB = a
Dễ thấy tứ giác ADCK là hình vuông => CK = a
∆ ACB có trung tuyến CK = 1 2 AB => ∆ ACB vuông tại C.
Ta có: 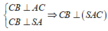
![]()
Trong (SAC) từ A hạ AH ⊥ SC tại H => AH ⊥ (SBC)
∆
SAC vuông tại A 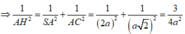
![]()
Cho hình chóp S.ABCD có đường cao SA = 2a, đáy ABCD là hình thang vuông ở A và D, AB=2a, AD = CD = a. Khoảng cách từ điểm A đến mặt phẳng (SBC) bằng
A. 2 a 3
B. 2 a 2
C. 2 a 3
D. a 2
Cho hình chóp S.ABCD có ABCD là hình thang vuông tại A và D, AB = AD =a,CD = 2a. Hình chiếu của S lên mặt phẳng (ABCD) trùng với trung điểm của BD. Biết thể tích tứ diện SBCD bằng a 3 6 . Tính khoảng cách từ A đến mặt phẳng (SBC) là:
A. a 3 2
B. a 2 6
C. a 3 6
D. a 6 4
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và D, đáy nhỏ của hình thang là CD, cạnh bên SC=a 15 . Tam giác SAD là tam giác đều cạnh bằng 2a và nằm trong mặt phẳng vuông góc với đáy. Gọi H là trung điểm AD, khoảng cách từ B đến mặt phẳng (SHC) bằng 2a 6 . Tính thể tích V của khối chóp S.ABCD?
![]()
![]()
![]()
![]()
Cho hình chóp S . A B C D có đáy là hình vuông tại A và D, S A ⊥ A B C D . Góc giữa SB và mặt phẳng đáy bằng 45 o . E là trung điểm của SD, A B = 2 a , A D = D C = a . Tính khoảng cách từ điểm B đến mặt phẳng A C E
A. 2 a 3
B. 4 a 3
C. a
D. 3 a 4
Cho hình chóp S.ABCD có đáy là hình thang cân với đáy A B = 2 a , A D = B C = C D = a , mặt bên SAB là tam giác cân đỉnh S và nằm trong mặt phẳng vuông góc với mặt phẳng (ABCD). Biết khoảng cách từ A tới mặt phẳng (SBC) bằng 2 a 15 5 , tính theo a thể tích V của khối chóp
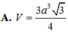
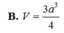
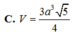
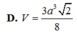
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A, B và AD = 2a, AB = BC = SA = a. Cạnh bên SA vuông góc với đáy, với M là trung điểm AD. Tính khoảng cách h từ M đến mặt phẳng (SCD).
A. h = a 3
B. h = a 6 6
C. h = a 6 3
D. h = a 3 6
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB=a, AD=2a, tam giác SAB cân tại S và nằm trong mặt phẳng vuông góc với đáy. Khoảng cách từ D đến (SBC) bằng 2 a 3 . Tính khoảng cách giữa hai đường thẳng SB và AC
A. a 10 10
B. a 10 5
C. 2 a 10 5
D. 2 a 5 5
Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B; AB = BC = a, AD = 2a, SA ⊥ (ABCD). Góc giữa mặt phẳng (SCD) và (ABCD) bằng 45 ∘ . Gọi M là trung điểm AD. Tính theo a thể tích V khối chóp S.MCD và khoảng cách d giữa hai đường thẳng SM và BD
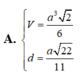
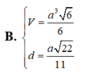
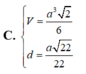
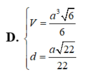
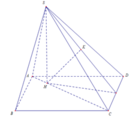
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành, A B = a , A C = a 3 , B C = 2 a . Tam giác SBC cân tại S, tam giác SCD vuông tại C. Khoảng cách từ D đến mặt phẳng (SBC) bằng a 3 3 . Chiều cao SH của hình chóp là
A. a 15 5
B. a 15 3
C. 2 a 15
D. a 5 3