Các câu hỏi tương tự
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật có
A
B
a
,
B
C
2
a
và
S
A
S
C
và
S
B
S
D
. Cạnh SC tạo với mặt phẳng đáy một góc bằng
60
0
. Thể tích khối chóp S.ABCD bằng:
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật có A B = a , B C = 2 a và S A = S C và S B = S D . Cạnh SC tạo với mặt phẳng đáy một góc bằng 60 0 . Thể tích khối chóp S.ABCD bằng:
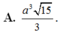
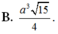
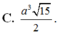
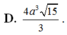
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, SA vuông góc với đáy và AB = a, AD=b, SA = c. Lấy các điểm B’, D’ theo thứ tự thuộc SB, SD sao cho AB’ vuông góc với SB, AD’ vuông góc với SD. Mặt phẳng (AB’D’) cắt SC tại C’. Tính thể tích khối chóp S.AB’C’D’.
Cho hình chóp S.ABCD có đáy là hình vuông ABCD cạnh a, SA vuông góc với đáy SA
a
2
. Gọi B, D là hình chiếu của A lần lượt lên SB, SD. Mặt phẳng cắt SC tại C. Thể tích khối chóp S.ABCD là:
Đọc tiếp
Cho hình chóp S.ABCD có đáy là hình vuông ABCD cạnh a, SA vuông góc với đáy SA= a 2 . Gọi B, D là hình chiếu của A lần lượt lên SB, SD. Mặt phẳng cắt SC tại C'. Thể tích khối chóp S.AB'C'D' là:
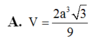
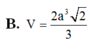
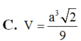
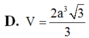
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với đáy,
S
A
a
2
. Gọi B’, D’ là hình chiếu của A lần lượt trên SB, SD. Mặt phẳng (AB’D’) cắt SC tại C’. Thể tích khối chóp S.AB’C’D’ là A.
V
2
a
3
3
3
B.
V...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với đáy, S A = a 2 . Gọi B’, D’ là hình chiếu của A lần lượt trên SB, SD. Mặt phẳng (AB’D’) cắt SC tại C’. Thể tích khối chóp S.AB’C’D’ là
A. V = 2 a 3 3 3
B. V = 2 a 3 2 3
C. V = 2 a 3 3 9
D. V = a 3 3 9
Cho hình chóp S.ABCD có đáy là hình vuông, SA vuông góc với đáy, SA = AC. Mặt phẳng qua A vuông góc với SC cắt SB, SC, SD lần lượt tại B', C', D'. Tỉ số giữa thể tích hình chóp S.A'B'C'D' và thể tích hình chóp S.ABCD là:
A. 1/6 B. 1/4
C. 1/3 D. 1/2
Cho hình chóp tứ giác đều S.ABCD có đáy ABCD là hình vuông cạnh bằng
a
3
và SASBSCSD
a
2
. Tính thể tích khối chóp S.ABCD. A.
2
a
3
6
B.
2
a
3
2
C....
Đọc tiếp
Cho hình chóp tứ giác đều S.ABCD có đáy ABCD là hình vuông cạnh bằng a 3 và SA=SB=SC=SD= a 2 . Tính thể tích khối chóp S.ABCD.
A. 2 a 3 6
B. 2 a 3 2
C. 3 a 3 3
D. 6 a 3 6
Hình chóp S.ABCD có đáy ABCD là hình chữ nhật, SA ⊥ (ABCD). Hạ AE ⊥ SB, AF ⊥ SD. Khi đó 5 điểm B, C, D, E, F cùng thuộc mặt cầu:
A. Đường kính SA.
B. Đường kính AC.
C. Đường kính SC.
D. Cả A, B, C đều sai.
Cho hình chóp S. ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với đáy, SA a
2
. Một mặt phẳng đi qua A vuông góc với SC cắt SB, SD, SC lần lượt tại B, D, C. Thể tích khối chóp S. ABCD là: A. V
2
a
3
3
9
B. V
2
a...
Đọc tiếp
Cho hình chóp S. ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với đáy, SA = a 2 . Một mặt phẳng đi qua A vuông góc với SC cắt SB, SD, SC lần lượt tại B', D', C'. Thể tích khối chóp S. AB'C'D' là:
A. V = 2 a 3 3 9
B. V = 2 a 3 2 3
C. V = a 3 2 9
D. V = 2 a 3 3 3
cho hình chóp sabcd có đáy abcd là hình chữ nhật,ab=a,ad=2a,sa vuông góc với mặt phẳng đáy,góc giữa sb và đáy bằng 45 độ,độ dài cạnh sd là







