Các câu hỏi tương tự
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi K,M lần lượt là trung điểm của các đoạn thẳng SA, SB,
α
là mặt phẳng qua K song song với AC và AM. Mặt phẳng
α
chia khối chóp S.ABCD thành hai khối đa diện. Gọi V1 là thể tích của khối đa diện chứa đỉnh S và V2 là thể tích khối đa diện còn lại. Tính tỉ số
V
1
V
2
.
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi K,M lần lượt là trung điểm của các đoạn thẳng SA, SB, α là mặt phẳng qua K song song với AC và AM. Mặt phẳng α chia khối chóp S.ABCD thành hai khối đa diện. Gọi V1 là thể tích của khối đa diện chứa đỉnh S và V2 là thể tích khối đa diện còn lại. Tính tỉ số V 1 V 2 .
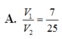
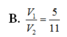
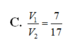
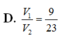
Cho hình chóp S. ABCD có đáy ABCD là hình thoi và có thể tích bằng 2. Gọi M, N lần lượt là các điểm trên cạnh SB và SD sao cho
S
M
S
B
S
N
S
D
k
. Tìm giá trị của k để thể tích khối chóp S.AMN bằng
1
8
A.k
1
8
B.k ...
Đọc tiếp
Cho hình chóp S. ABCD có đáy ABCD là hình thoi và có thể tích bằng 2. Gọi M, N lần lượt là các điểm trên cạnh SB và SD sao cho S M S B = S N S D = k . Tìm giá trị của k để thể tích khối chóp S.AMN bằng 1 8
A.k = 1 8
B.k = 2 2
C.k = 2 4
D.k = 1 4
Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi K là trung điểm SC. Mặt phẳng (P) qua AK cắt các cạnh SB, SD lần lượt tại M, N. Gọi V và V’ lần lượt là thể tích các khối chóp S.ABCD và S.AMKN. Tỉ số
V
V
có giá trị nhỏ nhất bằng A.
1
5
B.
3
8
C.
1
3
D.
1...
Đọc tiếp
Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi K là trung điểm SC. Mặt phẳng (P) qua AK cắt các cạnh SB, SD lần lượt tại M, N. Gọi V và V’ lần lượt là thể tích các khối chóp S.ABCD và S.AMKN. Tỉ số V ' V có giá trị nhỏ nhất bằng
A. 1 5
B. 3 8
C. 1 3
D. 1 2
Cho hình chóp tứ giác S.ABCD có thể tích bằng V. Lấy điểm A' trên cạnh SA sao cho SA' = SA/3. Mặt phẳng qua A' và song song với đáy của hình chóp cắt cạnh SB, SC, SD lần lượt tại B', C', D'. Thể tích hình chóp S.A'B'C'D' bằng:
A. V/3 B. V/9
C. V/27 D. V/81.
Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi K là trung điểm SC. Mặt phẳng AK cắt các cạnh SB, SD lần lượt tại M và N. Gọi
V
1
, V theo thứ tự là thể tích khối tứ diện S.AMKN và hình chóp S.ABCD. Giá trị nhỏ nhất của tỷ số
V
1
V
bằng: A.
1
2
B.
2
3
C. ...
Đọc tiếp
Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi K là trung điểm SC. Mặt phẳng AK cắt các cạnh SB, SD lần lượt tại M và N. Gọi V 1 , V theo thứ tự là thể tích khối tứ diện S.AMKN và hình chóp S.ABCD. Giá trị nhỏ nhất của tỷ số V 1 V bằng:
A. 1 2
B. 2 3
C. 1 3
D. 3 8
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M là điểm trên cạnh SC sao cho 5SM2SC mặt phẳng
(
α
)
qua A, M và song song với đường thẳng BD cắt hai cạnh SB, SD lần lượt tại H, K. Tính tỉ số thể tích
V
S
.
A
H
M
K
V
S...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M là điểm trên cạnh SC sao cho 5SM=2SC mặt phẳng ( α ) qua A, M và song song với đường thẳng BD cắt hai cạnh SB, SD lần lượt tại H, K. Tính tỉ số thể tích V S . A H M K V S . A B C D ?
A. 1 5
B. 8 35
C. 1 5
D. 6 35
Cho hình chóp S.ABCD có ABCD là hình vuông cạnh a,
S
D
a
17
2
Hình chiếu H của S lên mặt đáy là trung điểm của đoạn AB. Gọi K là trung điểm của AD. Thể tích của khối chóp S.HKDC là A.
5
a...
Đọc tiếp
Cho hình chóp S.ABCD có ABCD là hình vuông cạnh a, S D = a 17 2 Hình chiếu H của S lên mặt đáy là trung điểm của đoạn AB. Gọi K là trung điểm của AD. Thể tích của khối chóp S.HKDC là
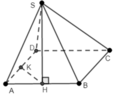
A. 5 a 3 3 8
B. 5 a 3 3 16
C. 5 a 3 3 24
D. 5 a 3 3 32
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M là điểm trên cạnh SC sao cho
5
S
M
2
S
C
, mặt phẳng
(
α
)
đi qua A, M và song song với đường thẳng BD cắt hai cạnh SB, SD lần lượt tại hai điểm H, K. Tính tỉ số thể tích
V
S
.
A
H
M
K...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M là điểm trên cạnh SC sao cho 5 S M = 2 S C , mặt phẳng ( α ) đi qua A, M và song song với đường thẳng BD cắt hai cạnh SB, SD lần lượt tại hai điểm H, K. Tính tỉ số thể tích V S . A H M K V S . A B C D .
A. 1 5
B. 8 35
C. 1 5
D. 6 35
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Hai điểm M, N thuộc các cạnh AB và AD (M, N không trùng với A) sao cho
A
B
A
M
+
2
A
D
A
N
4
. Kí hiệu
V
,
V
1
lần lượt là thể tích các khối...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Hai điểm M, N thuộc các cạnh AB và AD (M, N không trùng với A) sao cho A B A M + 2 A D A N = 4 . Kí hiệu V , V 1 lần lượt là thể tích các khối chóp S.ABCD và S.MBCDN. Tìm giá trị lớn nhất của tỉ số V 1 V
A. 3 4
B. 17 14
C. 1 6
D. 2 3



