Tam giác SBC là tam giác vuông tại B vì : AB là hình chiếu của SB trên (ABCD), mà BC ⊥ AB (do ABCD là hình vuông) ⇒ BC ⊥ SB (theo định lí ba đường vuông góc) ⇒ tam giác SBC là tam giác vuông
Đáp án D
Tam giác SBC là tam giác vuông tại B vì : AB là hình chiếu của SB trên (ABCD), mà BC ⊥ AB (do ABCD là hình vuông) ⇒ BC ⊥ SB (theo định lí ba đường vuông góc) ⇒ tam giác SBC là tam giác vuông
Đáp án D
Cho hình chóp S.ABCD có ABCD là hình vuông cạnh a, SA vuông góc với đáy (ABCD) và SAC là tam giác vuông cân. Thể tích Vcủa khối chóp S.ABCD bằng
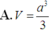
![]()
![]()
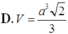
Cho hình chóp S.ABCD có đáy ABCD là một hình thoi cạnh a và có SA = SB = SC = a. Chứng minh rằng:
a) Mặt phẳng (ABCD) vuông góc với mặt phẳng (SBD).
b) Tam giác SBD là tam giác vuông.
Cho hình chóp S.ABCD có ABCD là hình vuông và SA ⊥ (ABCD) Tam giác SOD là:
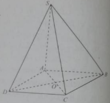
A. Tam giác thường
B. Tam giác cân
C. Tam giác đều
D. Tam giác vuông
Hình chóp S.ABCD có đáy là hình thoi ABCD cạnh a và có SA = SB = SC = a. Chứng minh:
a) Mặt phẳng (ABCD) vuông góc với mặt phẳng (SBD);
b) Tam giác SBD là tam giác vuông tại S.
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB=a Cạnh bên SA vuông góc với mặt phẳng đáy. Trong các tam giác sau, tam giác nào không phải là tam giác vuông?
A. △ S A B
![]()
![]()
![]()
Cho hình chóp S.ABCD có ABCD là hình chữ nhật. SA vuông góc với (ABCD), AH và AK lần lượt là đường cao của tam giác SAB và SAD.
Hai mặt phẳng (SAB) và (SBC) vuông góc vì.
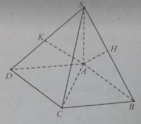
A. Góc của (SAB) và (SBC) là góc ABC và bằng 90 o .
B. Góc của (SAB) và (SBC) là góc BAD và bằng 90 o .
C. AB ⊥ BC; AB ⊂ (SAB) và BC ⊂ (SBC)
D. BC ⊥ (SAB) do BC ⊥ AB và BC ⊥ SA
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B, SA=\(a\sqrt{2}\), AC=2a và SA⊥(ABCD). Tính góc giữa 2 mp (SBC) và (ABC)
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A. Mặt bên SBC là tam giác đều cạnh a và (SBC) vuông góc với mặt đáy. Tính theo a khoảng cách giữa hai đường thẳng SA và BC.
A. a 3 8
B. a 6 4
C. a 3 4
D. a 3 2
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và D, AD=DC=a. Biết SAB là tam giác đều cạnh 2a và mặt phẳng (SAB) vuông góc với mặt phẳng (ABCD). Tính cosin của góc giữa hai mặt phẳng (SAB) và (SBC).
A. 2 7
B. 2 6
C. 3 7
D. 5 7