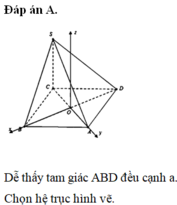
Các câu hỏi tương tự
Cho h̀nh chóp đều S.ABCD có đáy ABCD là h̀nh vuông cạnh
a
2
biết các cạnh bên tạo với đáy góc
60
0
.
Giá trị lượng giác tang của góc giữa hai mặt phẳng (SAC) và (SCD) bằng A.
2
3
3
B.
21
3
C.
21...
Đọc tiếp
Cho h̀nh chóp đều S.ABCD có đáy ABCD là h̀nh vuông cạnh a 2 biết các cạnh bên tạo với đáy góc 60 0 . Giá trị lượng giác tang của góc giữa hai mặt phẳng (SAC) và (SCD) bằng
A. 2 3 3
B. 21 3
C. 21 7
D. 3 2
Cho hình chóp S.ABCD có đáy là hình thoi ABCD cạnh a, có góc
B
A
D
^
60
o
và
S
A
S
B
S
D
a
3
2
a) Tính khoảng cách từ S đến mặt...
Đọc tiếp
Cho hình chóp S.ABCD có đáy là hình thoi ABCD cạnh a, có góc B A D ^ = 60 o và S A = S B = S D = a 3 2
a) Tính khoảng cách từ S đến mặt phẳng (ABCD) và độ dài cạnh SC.
b) Chứng minh mặt phẳng (SAC) vuông góc với mặt phẳng (ABCD).
c) Chứng minh SB vuông góc với BC.
d) Gọi φ là góc giữa hai mặt phẳng (SBD) và (ABCD). Tính tanφ.
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, góc
A
B
C
^
60
°
. Biết SA SB SC a. Góc giữa hai mặt phẳng (SBD) và (ABCD) bằng: A.
60
°
B.
30
°
C.
45
°
D.
90
°
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, góc A B C ^ = 60 ° . Biết SA = SB = SC = a. Góc giữa hai mặt phẳng (SBD) và (ABCD) bằng:
A. 60 °
B. 30 °
C. 45 °
D. 90 °
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a cạnh bên SA a và vuông góc với đáy. Côsin góc giữa đường thẳng SC và mặt (SBD) bằng A.
1
3
B.
2
3
C.
5...
Đọc tiếp
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a cạnh bên SA = a và vuông góc với đáy. Côsin góc giữa đường thẳng SC và mặt (SBD) bằng
A. 1 3
B. 2 3
C. 5 3
D. 2 2 3
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA a vuông góc với đáy. Côsin góc giữa đường thẳng SC và mặt phẳng (SBD) bằng A.
1
3
B.
2
2
3
C.
2
3
D.
5...
Đọc tiếp
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA =a vuông góc với đáy. Côsin góc giữa đường thẳng SC và mặt phẳng (SBD) bằng
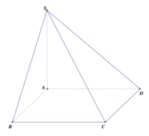
A. 1 3
B. 2 2 3
C. 2 3
D. 5 3
Hình chóp S.ABCD có đáy là hình thoi ABCD cạnh a và có SA = SB = SC = a. Chứng minh:
a) Mặt phẳng (ABCD) vuông góc với mặt phẳng (SBD);
b) Tam giác SBD là tam giác vuông tại S.
Cho hình chóp S.ABCD có đáy ABCD là một hình thoi cạnh a và có SA = SB = SC = a. Chứng minh rằng:
a) Mặt phẳng (ABCD) vuông góc với mặt phẳng (SBD).
b) Tam giác SBD là tam giác vuông.
Cho hình chóp S. ABCD có đáy ABCD là hình thoi cạnh a và A B C ^ = 60 ° . Hai mặt phẳng (SAC) và (SBD) cùng vuông góc với đáy, góc giữa hai mặt phẳng (SAB) và (ABCD) bằng 30 ° . Tính khoảng cách giữa hai đường thẳng SA, CD theo a ?
Bài 10. Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng 2a, cạnh bên bằng a * sqrt(3) . O là tâm hình vuông 1/ Chứng minh :a) (SAC) I (ABCD) b) (SAC) (SBD). 2 / a ) Tính d(S; (ABCD)) b) Tính d(O; (SCD)) 3/ Tính góc giữa:a) SC và (ABCD); b) (SAB) và (ABCD).