Các câu hỏi tương tự
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại C và SA
⊥
(ABC). Biết SA BC a, AB a
3
, tính khoảng cách h từ A tới mặt phẳng (SBC). A. h
a
3
2
B. h
a
3
2
C. h
a
2
3...
Đọc tiếp
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại C và SA ⊥ (ABC). Biết SA = BC = a, AB = a 3 , tính khoảng cách h từ A tới mặt phẳng (SBC).
A. h = a 3 2
B. h = a 3 2
C. h = a 2 3
D. h = a 2
Hình chóp S.ABC có SA ^ (ABC); SA AB AC a,
B
A
C
^
120
°
. Tính khoảng cách h từ A tới mặt phẳng (SBC). A. h
a
3
4
B. h
a
2
2
C. h
a...
Đọc tiếp
Hình chóp S.ABC có SA ^ (ABC); SA = AB = AC = a, B A C ^ = 120 ° . Tính khoảng cách h từ A tới mặt phẳng (SBC).
A. h = a 3 4
B. h = a 2 2
C. h = a 5
D. h = a 2
Hình chóp SABCD có SA
⊥
(ABC). Biết d(SA,BC) a, SA a
3
. Tính khoảng cách h từ A tới mặt phẳng (SBC) A. h
a
2
B. h
a
3
2
C. h
a
2
2
D. h
a
2
3
Đọc tiếp
Hình chóp SABCD có SA ⊥ (ABC). Biết d(SA,BC) = a, SA = a 3 . Tính khoảng cách h từ A tới mặt phẳng (SBC)
A. h = a 2
B. h = a 3 2
C. h = a 2 2
D. h = a 2 3
Cho hình chóp
S
.
A
B
C
có
S
A
⊥
A
B
C
,
∆
A
B
C
là tam giác đều cạnh a và tam giác SAB cân. Tính khoảng cách h từ điểm A đến mặt phẳng
S
B
C
. A.
h
a...
Đọc tiếp
Cho hình chóp S . A B C có S A ⊥ A B C , ∆ A B C là tam giác đều cạnh a và tam giác SAB cân. Tính khoảng cách h từ điểm A đến mặt phẳng S B C .
A. h = a 3 7
B. h = a 3 2
C. h = 2 a 7
D. h = a 3 7
Hình chóp S.ABC có (SBC)
⊥
(ABC), tam giác ABC đều cạnh a, tam giác SBC vuông cân tại S. Tính khoảng cách h từ SA đến BC theo a. A. h
a
4
B. h
a
3
2
C. h
a
3
4
D. h
a
2
2
Đọc tiếp
Hình chóp S.ABC có (SBC) ⊥ (ABC), tam giác ABC đều cạnh a, tam giác SBC vuông cân tại S. Tính khoảng cách h từ SA đến BC theo a.
A. h = a 4
B. h = a 3 2
C. h = a 3 4
D. h = a 2 2
Cho khối chóp S.ABC có SA
⊥
(ABC), tam giác ABC đều cạnh a và tam giác SAB cân. Tính khoảng cách h từ điểm A đến mặt phẳng (SBC).
Đọc tiếp
Cho khối chóp S.ABC có SA ⊥ (ABC), tam giác ABC đều cạnh a và tam giác SAB cân. Tính khoảng cách h từ điểm A đến mặt phẳng (SBC).
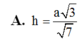
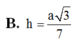
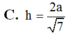
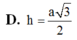
Hình chóp S.ABC có SA
⊥
(ABC), tam giác ABc đều cạnh a và góc giữa mặt phẳng (SBC) với mặt phẳng (ABC) bằng 60
°
. Tính khoảng cách h từ A tới mặt phẳng (SBC). A. h a
2
3
B. h
a
3
4
C. h
a
2
D. h
3
a...
Đọc tiếp
Hình chóp S.ABC có SA ⊥ (ABC), tam giác ABc đều cạnh a và góc giữa mặt phẳng (SBC) với mặt phẳng (ABC) bằng 60 ° . Tính khoảng cách h từ A tới mặt phẳng (SBC).
A. h = a 2 3
B. h = a 3 4
C. h = a 2
D. h = 3 a 4
Cho hình chóp S.ABC có BC a. Góc giữa hai mặt phẳng (SBC) và (ABC) bằng
60
o
Gọi H là hình chiếu vuông góc của đỉnh S trên mặt phẳng (ABC). Biết rằng tam giác HBC vuông cân tại H và thể tích khối chóp S.ABC bằng
a
3
Khoảng cách từ A đến mặt phẳng (SBC) bằng A.
2
a
3
B.
6
a
3
C. ...
Đọc tiếp
Cho hình chóp S.ABC có BC = a. Góc giữa hai mặt phẳng (SBC) và (ABC) bằng 60 o Gọi H là hình chiếu vuông góc của đỉnh S trên mặt phẳng (ABC). Biết rằng tam giác HBC vuông cân tại H và thể tích khối chóp S.ABC bằng a 3 Khoảng cách từ A đến mặt phẳng (SBC) bằng
A. 2 a 3
B. 6 a 3
C. 2 a
D. 6 a
Hình chóp S.ABC có SA
⊥
(ABC), AB 2a, AC 3a,
B
A
C
^
60
°
m góc giữa (SBC) và (ABC) bằng 45°. Tính khoảng cách h từ A xuống (SBC). A. h a
27
14
B. h a
7
2
C. h
3
a...
Đọc tiếp
Hình chóp S.ABC có SA ⊥ (ABC), AB = 2a, AC = 3a, B A C ^ = 60 ° m góc giữa (SBC) và (ABC) bằng 45°. Tính khoảng cách h từ A xuống (SBC).
A. h = a 27 14
B. h = a 7 2
C. h = 3 a 2
D. h = 6 a 2



