Chọn C.
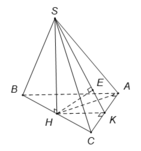
Gọi H là trung điểm của BC, suy ra .
![]()
Gọi K là trung điểm AC
![]()
![]()
![]()
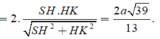
Chọn C.

Gọi H là trung điểm của BC, suy ra .
![]()
Gọi K là trung điểm AC
![]()
![]()
![]()
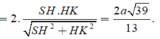
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B với AB = a và B A C ^ = 30 0 . Hai mặt phẳng (SAB) và (SAC) cùng vuông góc với mặt phẳng (ABC). Tính khoảng cách d từ điểm A đến mặt phẳng (SBC) biết khối chóp S.ABC có thể tích bằng a 3 3 36
A . d = a 2 5
B . d = a 3
C . d = a 5 5
D . d = a 3 6
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B , AB =a, BC =a 3 Biết rằng SA vuông góc với mặt phẳng đáy và diện tích xung quanh của khối chóp S.ABC bằng 5 a 2 3 2 . Tính theo a khoảng cách d từ A đến mặt phẳng (SBC) gần với giá trị nào nhất sau đây ?
A. 0,72a
B. 0,9a
C. 0,8a
D. 1,12a
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a. Cạnh bên SA = a 3 và vuông góc với mặt đáy (ABC). Tính khoảng cách d từ A đến mặt phẳng (SBC).
A. d = a 15 5
B. d = a
C. d = a 5 5
D. d = a 3 2
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, AB = 3a, BC = 4a, mặt phẳng (SBC) vuông góc với mặt phẳng (ABC). Biết SB = 2a 3 và S B C ^ = 30 0 . Tính khoảng cách từ B đến mặt phẳng (SAC) theo a.
A . 3 a 5
B . a 7
C . 6 a 7
D . 3 a 7
Cho hình chóp tam giác đều S.ABC có độ dài cạnh đáy bằng a, cạnh bên bằng a 3 . Gọi O là tâm đáy ABC, d 1 là khoảng cách từ A đến mặt phẳng (SBC) và d 2 là khoảng cách từ O đến mặt phẳng (SBC). Tính d = d 1 + d 2
A. d = 2 a 2 11
B. d = 2 a 2 33
C. d = 8 a 22 33
D. d = 8 a 2 11
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, SA vuông góc với đáy.
a) Chứng minh tam giác SBC vuông
b) Gọi H là chân đường cao vẽ từ B của tam giác ABC.
Chứng minh (SAC) ⊥ (SBH)
c) Cho AB = a, BC = 2a. Tính khoảng cách từ B đến mặt phẳng (SAC)
Cho chóp tứ giác S.ABCD có đáy là hình vuông cạnh 2a và tam giác SAD đều đồng thời nằm trong mặt phẳng vuông góc đáy. Tính khoảng cách d từ tâm đường tròn nội tiếp tam giác SAD đến mặt phẳng (SBC) theo a
A. d = 2 a 21 7
B. d = 4 a 57 57
C. d = 2 a 21 21
D. d = 4 a 21 21
Cho hình chóp S.ABC có đáy ABC vuông tại A, A B = a , A C = a 3 Tam giác SBC đều và nằm trong mặt phẳng vuông góc với mặt đáy. Tính thể tích khối chóp S.ABC.
A. 2 a 2 3
B. 3 a 2 2
C. a 3 3 2
D. a 2 2
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, tam giác SAC cân tại S và nằm trong mặt phẳng vuông góc với đáy, góc S B C ^ = 60 0 . Tính theo a thể tích khối chóp .
A . a 3 2 4
B . a 3 2 24
C . a 3 3 4
D . a 3 2 8