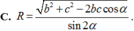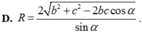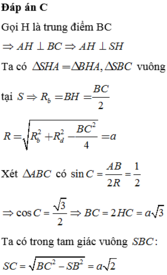Các câu hỏi tương tự
Cho hình chóp S.ABC có đáy ABC là tam giác cân tại A với ABACa, cạnh SASBa và có (SBC)
⊥
(ABC). Tính SC để độ dài bán kính mặt cầu ngoại tiếp hình chóp bằng a.
Đọc tiếp
Cho hình chóp S.ABC có đáy ABC là tam giác cân tại A với AB=AC=a, cạnh SA=SB=a và có (SBC) ⊥ (ABC). Tính SC để độ dài bán kính mặt cầu ngoại tiếp hình chóp bằng a.
Cho hình chóp S.ABC có đáy ABC là tam giác cân tại A với ABACa. Cạnh bên SASBa và có
S
B
C
⊥
A
B
C
. Tính độ dài SC để bán kính mặt cầu ngoại tiếp hình chóp bằng a A.
S
C
a
B.
S
C
a
2
C.
S
C
a...
Đọc tiếp
Cho hình chóp S.ABC có đáy ABC là tam giác cân tại A với AB=AC=a. Cạnh bên SA=SB=a và có S B C ⊥ A B C . Tính độ dài SC để bán kính mặt cầu ngoại tiếp hình chóp bằng a
A. S C = a
B. S C = a 2
C. S C = a 3
D. S C = 2 a
Cho hình chóp S. ABC có đáy ABC là tam giác cân tại A, biết AB a; SA SB a và mặt phẳng (SBC) vuông góc với mặt phẳng (ABC). Tính SC biết bán kính mặt cầu ngoại tiếp hình chóp S.ABC bằng a.
Đọc tiếp
Cho hình chóp S. ABC có đáy ABC là tam giác cân tại A, biết AB = a; SA = SB = a và mặt phẳng (SBC) vuông góc với mặt phẳng (ABC). Tính SC biết bán kính mặt cầu ngoại tiếp hình chóp S.ABC bằng a.
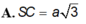
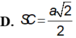
Cho hình chóp S.ABC có đáy ABC là tam giác cân tại A , mặt phẳng (SBC) vuông góc với mặt phẳng (ABC) và SASBABACa; SCa
2
. Diện tích xung quanh mặt cầu ngoại tiếp hình chóp S.ABC bằng: A. 2
πa
2
B.
πa
2
C. 8
πa
2
D. 4
πa
2
Đọc tiếp
Cho hình chóp S.ABC có đáy ABC là tam giác cân tại A , mặt phẳng (SBC) vuông góc với mặt phẳng (ABC) và SA=SB=AB=AC=a; SC=a 2 . Diện tích xung quanh mặt cầu ngoại tiếp hình chóp S.ABC bằng:
A. 2 πa 2
B. πa 2
C. 8 πa 2
D. 4 πa 2
Hình chóp A.BCD có đáy ABC là tam giác vuông tại a, SA vuông góc với mặt phẳng (ABC), SA a, AB b, AC c. Tính bán kính R của mặt cầu đi qua các điểm A, B, C và S ? A.
R
2
(
a
+
b
+
c
)...
Đọc tiếp
Hình chóp A'.BC'D có đáy ABC là tam giác vuông tại a, SA vuông góc với mặt phẳng (ABC), SA = a, AB = b, AC = c. Tính bán kính R của mặt cầu đi qua các điểm A, B, C và S ?
A. R = 2 ( a + b + c ) 3
B. R = 2 a 2 + b 2 + c 2
C. R = 1 2 a 2 + b 2 + c 2
D. R = a 2 + b 2 + c 2
Cho hình chóp S.ABC có đáy ABC là tam giác cân tại B, ABBCa và
∠
A
B
C
120
°
. Cạnh bên SA vuông góc với mặt phẳng đáy và SA2a. Tính theo a bán kính mặt cầu ngoại tiếp hình chóp S.ABC. A.
a
2
5
B. ...
Đọc tiếp
Cho hình chóp S.ABC có đáy ABC là tam giác cân tại B, AB=BC=a và ∠ A B C = 120 ° . Cạnh bên SA vuông góc với mặt phẳng đáy và SA=2a. Tính theo a bán kính mặt cầu ngoại tiếp hình chóp S.ABC.
A. a 2 5
B. a 2
C. a 5
D. a 2 4
Cho hình chóp S.ABC có
S
A
⊥
(
A
B
C
)
, AC b, AB c, . Gọi B, C lần lượt là hình chiếu vuông góc của A lên SB, SC. Tính bán kính mặt cầu ngoại tiếp hình chóp A.BCCB theo b, c,
α
.
Đọc tiếp
Cho hình chóp S.ABC có
S
A
⊥
(
A
B
C
)
, AC = b, AB = c, 
. Gọi B', C' lần lượt là hình chiếu vuông góc của A lên SB, SC. Tính bán kính mặt cầu ngoại tiếp hình chóp A.BCC'B' theo b, c,
α
.
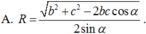
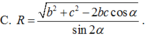
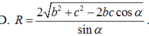
Cho hình chóp S.ABCD có tam giác ABC cân tại A, cạnh bên là a. Biết rằng khoảng cách từ đỉnh S tới mặt đáy (ABC) bằng hai lần đường cao kẻ từ đỉnh A của tam giác ABC đồng thời các vuông tại B và C. Tìm giá trị nhỏ nhất của bán kính mặt cầu ngoại tiếp tứ diện S.ABC
Đọc tiếp
Cho hình chóp S.ABCD có tam giác ABC cân tại A, cạnh bên là a. Biết rằng khoảng cách từ đỉnh S tới mặt đáy (ABC) bằng hai lần đường cao kẻ từ đỉnh A của tam giác ABC đồng thời các vuông tại B và C. Tìm giá trị nhỏ nhất của bán kính mặt cầu ngoại tiếp tứ diện S.ABC
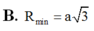
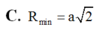
Cho hình chóp S.ABC có
S
A
⊥
(
A
B
C
)
, ACb, ABc,
B
A
C
^
α
. Gọi B, C lần lượt là hình chiếu vuông góc của A lên SB, SC. Tính bán kính mặt cầu ngoại tiếp hình chóp A.BCCB theo b, c,
α
.
Đọc tiếp
Cho hình chóp S.ABC có S A ⊥ ( A B C ) , AC=b, AB=c, B A C ^ = α . Gọi B', C' lần lượt là hình chiếu vuông góc của A lên SB, SC. Tính bán kính mặt cầu ngoại tiếp hình chóp A.BCC'B' theo b, c, α .
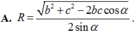
