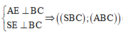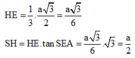Các câu hỏi tương tự
Câu 1. Cho hình chóp S ABC . có SA vuông góc với ABC và đáy ABC đều cạnh a. Biết SA3a/2.Gọi H là trung điểm của BC.a. Tính góc giữa hai mặt phẳng SBC và ABC ?b. Tính diện tích của tam giác ABC từ đó suy ra diện tích tam giác SBC ?c. Chứng minh SBC vuông góc với SAH Câu 2. Cho hình chóp tam giác đều S ABC . có cạnh đáy bằng a và đường cao SH bằng cạnh đáy. Tính số đo góc hợp bởi mặt bên và mặt đáy
Đọc tiếp
Câu 1. Cho hình chóp S ABC . có SA vuông góc với ABC và đáy ABC đều cạnh a. Biết SA=3a/2.Gọi H là trung điểm của BC.
a. Tính góc giữa hai mặt phẳng SBC và ABC ?
b. Tính diện tích của tam giác ABC từ đó suy ra diện tích tam giác SBC ?
c. Chứng minh SBC vuông góc với SAH
Câu 2. Cho hình chóp tam giác đều S ABC . có cạnh đáy bằng a và đường cao SH bằng cạnh đáy. Tính số đo góc hợp bởi mặt bên và mặt đáy
Cho hình chóp S.ABC có đáy là tam giác đều cạnh a. Hình chiếu vuông góc của S trên mặt phẳng (ABC) là điểm H thuộc cạnh AB sao cho HA 3HB. Góc giữa đường thẳng SC và mặt phẳng bằng 60°. Tính khoảng cách giữa hai đường thẳng SA và BC theo a.
A
.
a
61
4
B
.
4
a
17...
Đọc tiếp
Cho hình chóp S.ABC có đáy là tam giác đều cạnh a. Hình chiếu vuông góc của S trên mặt phẳng (ABC) là điểm H thuộc cạnh AB sao cho HA = 3HB. Góc giữa đường thẳng SC và mặt phẳng bằng 60°. Tính khoảng cách giữa hai đường thẳng SA và BC theo a.
A . a 61 4
B . 4 a 17 3
C . a 35 51
D . 4 a 351 3 61
Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng 1, góc giữa cạnh bên và mặt đáy bằng 60
o
C
. Gọi A,B,C lần lượt là các điểm đối xứng của A,B,C qua S. Thể tích của khối đa diện ABCABC bằng A.
V
2
3
3
B.
V...
Đọc tiếp
Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng 1, góc giữa cạnh bên và mặt đáy bằng 60 o C . Gọi A',B',C' lần lượt là các điểm đối xứng của A,B,C qua S. Thể tích của khối đa diện ABCA'B'C' bằng
A. V = 2 3 3
B. V = 2 3
C. V = 4 3 3
D. V = 3 2
Cho hình chóp tam giác đều S. ABC có độ dài cạnh đáy bằng a. Độ dài cạnh bên của hình chóp bằng bao nhiêu để góc giữa cạnh bên và mặt đáy bằng
60
0
? A.
2
a
3
B.
a
6
C.
a
3
6
D. ...
Đọc tiếp
Cho hình chóp tam giác đều S. ABC có độ dài cạnh đáy bằng a. Độ dài cạnh bên của hình chóp bằng bao nhiêu để góc giữa cạnh bên và mặt đáy bằng 60 0 ?
A. 2 a 3
B. a 6
C. a 3 6
D. 2 a 3
Cho hình chóp đều S.ABC có cạnh đáy bằng a, cạnh bên hợp với mặt đáy một góc
60
o
Gọi (S ) là mặt cầu ngoại tiếp hình chóp S.ABC. Thể tích của khối cầu tạo nên bởi mặt cầu (S ) bằng
Đọc tiếp
Cho hình chóp đều S.ABC có cạnh đáy bằng a, cạnh bên hợp với mặt đáy một góc 60 o Gọi (S ) là mặt cầu ngoại tiếp hình chóp S.ABC. Thể tích của khối cầu tạo nên bởi mặt cầu (S ) bằng
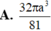
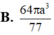
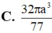
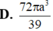
Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a và đường cao SH bằng cạnh đáy. Tính số đo góc hợp bởi cạnh bên và mặt đáy.
Bài 4. Cho hình chóp S.ABC , hình chiếu của S lên mặt phẳng (ABC) là trung điểm H của AC, đáy ABC là tam giác vuông ở B, SA = 2a, AB = av3, BC = a. Tính góc (SH,(SAB)). Bài 5. Cho hình chóp S.ABCD, SA1(ABCD), đáy ABCD là hình vuông cạnh a, góc giữa mặt phăng (SBC) và (ABCD) bằng 30°. Tính góc (AD.(SCD)).
Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng 2a , góc giữa cạnh bên và mặt đáy bằng
60
°
. Khoảng cách từ điểm S đến mặt đáy (ABC) là
Đọc tiếp
Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng 2a , góc giữa cạnh bên và mặt đáy bằng 60 ° . Khoảng cách từ điểm S đến mặt đáy (ABC) là
![]()
![]()
![]()
![]()
Cho hình chóp tam giác đều S. ABC có độ dài cạnh đáy bằng a, góc hợp bởi cạnh bên và mặt đáy bằng
60
0
.Tính thể tích khối chóp đã cho A.
3
12
a
3
B.
3
a
3
6
C. ...
Đọc tiếp
Cho hình chóp tam giác đều S. ABC có độ dài cạnh đáy bằng a, góc hợp bởi cạnh bên và mặt đáy bằng 60 0 .Tính thể tích khối chóp đã cho
A. 3 12 a 3
B. 3 a 3 6
C. 3 3 a 3
D. 3 4 a 3