Các câu hỏi tương tự
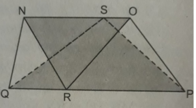
Cho hình bs.30 (hình bình hành MNPQ có diện tích S và X, Y tương ứng là trung điểm của các cạnh QP, PN). Khi đó, diện tích của tứ giác MXPY bằng:
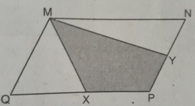
(A) 1/4 S;
(B) 1/2 S;
(C) 1/8 S;
(D) 3/4 S.
Cho hình bs.29, trong đó HK = KF = FL = LT và tam giác GHT có diện tích S. Khi đó, diện tích của tam giác GKL bằng:
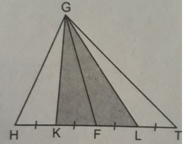
(A) 1/2 S;
(B) 1/4 S;
(C) 1/8 S;
(D) 3/4 S.
Trong 1 hình tròn có diện tích S lấy 2017 điểm bất kì. C/m ít nhất có 3 điểm tạo thành 1 tam giác mà diện tích S< S/1008
Bài 1: Chứng minh rằng: Tổng khoảng cách từ 1 điểm bất kì trong tam giác đều đến 3 cạnh của 1 tam giác không phụ thuộc vào vị trí điểm đó trong tam giácBài 2: Cho tam giác ABC, điểm M trong tam giác sao cho S tam giác AMB + S tam giác BMC S tam giác MAC di chuyển trên đường nào?(a)b) Các điểm I sao cho S AIC S tam giác ABC di chuyển trên đường nào?c) Các điểm O sao cho S ADC2S ABC di chuyển trên đường nào?Bài 3: Trong các hình chữ nhật có cùng S100cm^2. Hình nào có chu vi nhỏ nhất
Đọc tiếp
Bài 1: Chứng minh rằng: Tổng khoảng cách từ 1 điểm bất kì trong tam giác đều đến 3 cạnh của 1 tam giác không phụ thuộc vào vị trí điểm đó trong tam giác
Bài 2: Cho tam giác ABC, điểm M trong tam giác sao cho S tam giác AMB + S tam giác BMC= S tam giác MAC di chuyển trên đường nào?(a)
b) Các điểm I sao cho S AIC = S tam giác ABC di chuyển trên đường nào?
c) Các điểm O sao cho S ADC=2S ABC di chuyển trên đường nào?
Bài 3: Trong các hình chữ nhật có cùng S=100cm^2. Hình nào có chu vi nhỏ nhất
Cho tam giác ABC , A= 90 độ . đường cao AH. người ta kẻ đường cao HI,HK của tam giác ABH và tam giác AHC . Gọi Mvà N là trung điểm của BH và CH.
a, cm : HI đi qua trung điểm của AH
b, cm:tứ giác MNKI là hình thang .
c, cm: diện tích hình thang MNKI = 1/2 tam giác ABC
d,các tia HI,HK cắt đường thẳng bất kì qua A ở T,S
cm: BT // CS
các bạn làm giúp tôi câu c và d nha .
1 Cho ABCD là hình thang cân ( AB // CD ; ABCD) biết AB 8cm , CD2AB ; AH vuông góc với CD và AH 3 cm . Chu vi hình thang ABCD là 2 Cho hình vuông ABCD có diện tích 36cm2 Gọi M ; N lần lượt là trung điểm của các cạnh BC và CD . Khi đó diện tích tam giác AMN là ............ cm23 Cho hình vuông ABCD có AB 16cm . AC cắt BD tại O ; 1 góc vuông xOy có tia Ox cát cạnh AB tại E và tia Oy cát cạnh BC tại E . Diện tích tứ giác OEBF là ??????4 Cho tam giác ABC gọi D là trung điểm của cạnh BC ; E là 1 đ...
Đọc tiếp
1 Cho ABCD là hình thang cân ( AB // CD ; AB<CD) biết AB = 8cm , CD=2AB ; AH vuông góc với CD và AH = 3 cm . Chu vi hình thang ABCD là
2 Cho hình vuông ABCD có diện tích = 36cm2 Gọi M ; N lần lượt là trung điểm của các cạnh BC và CD . Khi đó diện tích tam giác AMN là ............ cm2
3 Cho hình vuông ABCD có AB =16cm . AC cắt BD tại O ; 1 góc vuông xOy có tia Ox cát cạnh AB tại E và tia Oy cát cạnh BC tại E . Diện tích tứ giác OEBF là ??????
4 Cho tam giác ABC gọi D là trung điểm của cạnh BC ; E là 1 điểm bất kỳ trên cạnh AC (E khác A ) và F là trung điểm của BE nếu SABC =120cm2 và SAFDC = 80 cm2 thì SBDF là ................. cm2
5 Cho tam giác ABC có diện tích 20 cm2 gọi AM là trung tuến của tam giác khi đó SABM là ..............cm2
GIÚP MK NHANH NHA MN KẾT QUẢ THÔI CŨNG DƯỢC
Câu hỏi: Cho hình chữ nhật ABCD . O là giao điểm của hai đường chéo và 1 điểm P bất kì trên đường chéo BD (P nằm giữa O và D) . Gọi M là điểm đối xứng của C qua P a)Cm: AMDB là hình thang. XÁc định vị trí của P trên BD để AMDB là hình thang cân b)Trên cạnh AB lấy điểm X, trên cạnh DC lấy điểm J sao cho AXCJ, N là điểm tùy ý trên cạnh AD . Gọi G, H thứ tự là giao điểm của XJ với NB, NC 1/ tính diện tích tứ giác AXJD theo diện tích ABCDs 2/ Cm: diện tích AXGN+diện tích NHJDdiện tích GBCH d) gọi K...
Đọc tiếp
Câu hỏi: Cho hình chữ nhật ABCD . O là giao điểm của hai đường chéo và 1 điểm P bất kì trên đường chéo BD (P nằm giữa O và D) . Gọi M là điểm đối xứng của C qua P a)Cm: AMDB là hình thang. XÁc định vị trí của P trên BD để AMDB là hình thang cân b)Trên cạnh AB lấy điểm X, trên cạnh DC lấy điểm J sao cho AX=CJ, N là điểm tùy ý trên cạnh AD . Gọi G, H thứ tự là giao điểm của XJ với NB, NC 1/ tính diện tích tứ giác AXJD theo diện tích ABCD=s 2/ Cm: diện tích AXGN+diện tích NHJD=diện tích GBCH d) gọi K là điểm trên cạnh AB sao cho góc ADK=15 độ và AB=2 BC. Cm: tam giác CDK cân
Bài 1: Cho tam giác ABC cân ở A. Các đường thẳng qua đỉnh B,C và trung điểm O của đường cao tương ứng với đỉnhA cắt các cạnh AB, AC tương ứng tại M, N. Biết diện tích tam giác ABC bằng S, tính diện tích tứ giác AMON?Bài 2: Cho tứ giác ABCD, M và N lần lượt là trung điểm của BC và AD. AM cắt BN ở I, DM cắt CN ở J. Chứng minh rằng: SMINJSABI+SCBJBài 3: Cho tam giác ABC có AB3cm, BC4cm, CA5cm. Đường cao, đường phân giác, đường trung tuyến của tam giác ABC kẻ từ đỉnh B chia tam giác thành 4 phần. Tí...
Đọc tiếp
Bài 1: Cho tam giác ABC cân ở A. Các đường thẳng qua đỉnh B,C và trung điểm O của đường cao tương ứng với đỉnhA cắt các cạnh AB, AC tương ứng tại M, N. Biết diện tích tam giác ABC bằng S, tính diện tích tứ giác AMON?
Bài 2: Cho tứ giác ABCD, M và N lần lượt là trung điểm của BC và AD. AM cắt BN ở I, DM cắt CN ở J. Chứng minh rằng: SMINJ=SABI+SCBJ
Bài 3: Cho tam giác ABC có AB=3cm, BC=4cm, CA=5cm. Đường cao, đường phân giác, đường trung tuyến của tam giác ABC kẻ từ đỉnh B chia tam giác thành 4 phần. Tính diện tích mỗi phần?
Bài 4: Cho tam giác ABC có diện tích 30cm2. trên cạnh AB lấy điểm D sao cho AD=2DB, trên cạnh AC lấy điểm E sao cho AE=3EC. Gọi M là giao điểm của BE và CD. Tính diện tích tam giác AMB?
Cho hình chữ nhật ABCD có O là giao điểm hai đường chéo AC và BD . Lấy điểm P trên cạnh BD ( P nằm giữa O và D ). Gọi M là điểm đối xứng với C qua P.a) Chứng minh AMDB là hình thang. Xác định vị trí điểm P trên BD để AMBD là hình thang cân.b) Kẻ ME vuông góc AD, MF vuông góc AB. Chứng minh rằng EF // AC và E, F, P thẳng hàng.c) Trên cạnh AB lấy điểm X , trên DC lấy điểm J sao cho AXCJ, lấy N là điểm tùy ý trên AD. Gọi G là giao điểm của XJ và NB, H là giao điểm của XJ và NC . Tính diện tích của...
Đọc tiếp
Cho hình chữ nhật ABCD có O là giao điểm hai đường chéo AC và BD . Lấy điểm P trên cạnh BD ( P nằm giữa O và D ). Gọi M là điểm đối xứng với C qua P.
a) Chứng minh AMDB là hình thang. Xác định vị trí điểm P trên BD để AMBD là hình thang cân.
b) Kẻ ME vuông góc AD, MF vuông góc AB. Chứng minh rằng EF // AC và E, F, P thẳng hàng.
c) Trên cạnh AB lấy điểm X , trên DC lấy điểm J sao cho AX=CJ, lấy N là điểm tùy ý trên AD. Gọi G là giao điểm của XJ và NB, H là giao điểm của XJ và NC . Tính diện tích của tứ giác AXJD theo diện tích ABCD =S. Chứng minh rằng S AXGN + S NHJD = S GBCH
d) Gọi K là điểm thuộc cạnh AB sao cho góc ADK = 15 độ và AB = 2BC . Chứng minh tam giác CDK cân