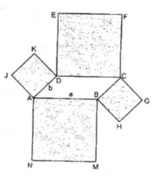
Hình đa giác đó gồm hình bình hành ABCD, hình vuông ABMN, BHGC, CFED, DKJA.
S A B M N = S C D E F = a 2
S B H G C = S D K J A = b 2
Diện tích đa giác bằng :
S A B M N = S C D E F = a 2
S B H G C = S D K J A = b 2
Đúng 1
Bình luận (0)
Các câu hỏi tương tự
Cho hình bình hành ABCD, với diện tích S và AB = a, AD = b. Lấy mỗi cạnh của hình bình hành đó làm cạnh dựng một hình vuông ra phía ngoài hình bình hành. Tính thep a, b cad S diện tích của đa giác giới hạn bởi các cạnh của hình vuông mà không là cạnh của hình bình hành đã cho ?
Cho hình bình hành ABCD . Vẽ ra phía ngoài của hình bình hành các hình vuông có một cạnh là
cạnh của hình bình hành. Gọi E,F,G,H lần lượt là tâm (tức là giao điểm của hai đường chéo) của
các hình vuông vẽ trên các cạnh AB,BC,CD và DA. Chứng minh rằng: EG = HF và EG ⊥ HF.
Cho hình bình hành ABCD vẽ bốn điểm P,Q,R,S của các cạnh CD,AD,AB và BC. chứng minh tứ giác tạo bởi các dường thẳng này có diện tích bằng 1/5 dieenh tích hình bình hành ABCD
cho hình bình hành abcd, ở phía ngoài của hình bình hành vẽ 4 hình vuông có cạnh là các cạnh của hình bình hành. cmr tâm của các hình vuông là đỉnh của 1 hình vuông khác
1. Cho hình vuông ABCD có độ dài cạnh là 6cm. Trên cạnh AB lấy điểm E sao cho diện tích hình vuông ABCD gấp 3 lần diện tích tam giác ADE. Tính AE.
2. Tính số đo các góc của hình bình hành ABCD. Biết A+B+C=230
Cho hình bình hành ABCD. Dựng hình bình hành thứ 2 nhận CD làm cạnh và có diện tích bằng diện tích hình bình hành đã cho. Có thể dựng được bao nhiêu hình bình hành như thế
Cho hình bình hành ABCD có cạnh AB = 10 3 c m , AD = 8cm, A ^ = 60°. Tính diện tích của hình bình hành
cho hình bình hành ABCD có AB bằng 20cm ad bằng 15 cm , góc tạo bởi hai cạnh AB và BD là 120 độ .Tính diện tích hình bình hành ABCD
Cho hình bình hành ABCD, ab=2ad. gọi E,F theo thứ tự là trung điểm của AB và CD
a) c/m tứ giác AECF là hình bình hành
b) c/m AF vuông góc DE
c) Gọi M là giao điểm của AF và DE, N là giao điểm của BF và CE.c/m EF=MN
d) Tính tỷ số diện tích của tam giác BEF và diện tích hình bình hành ABCD
Xem chi tiết