Các câu hỏi tương tự
Cho hình bình hành ABCD. Trên đường chéo AC lấy các điểm M,N sao cho AM = CN. Trên AB lấy điểm E, trên CD lấy điểm F sao cho BF = DE. Chứng minh rằng : MENF là hình bình hành
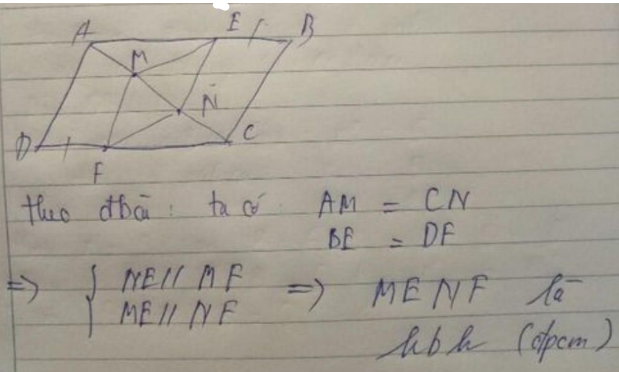
cho hình bình hành ABCD, trên đường chéo AC lấy M,N sao cho AM=CN. Lấy E thuộc AB, lấy F thuộc DC sao cho BE=DF. CM: MENF là hình bình hành.
Cho hình bình hành ABCD. Trên cạnh AB lấy điểm E và trên cạnh CD lấy điểm F sao cho AE = CF. Trên cạnh AD lấy điểm M và trên cạnh BC lấy điểm N sao cho AM = CN.
a) Tứ giác MENF là hình gì? Vì sao?
b) Chứng minh các đường thẳng AC;BD;EF và MN đồng quy tại 1 điểm.
Cho hình bình hành ABCD. Trên tia AB và CD lấy 2 điểm E và F sao cho AE = CF và trên AD và BC lấy 2 điểm M và N sao cho AM=CN.
a) Tứ giác MENF là hình gì? Vì sao ?
b) Chứng minh rằng các đường thẳng AC,BD,EF,MN đồng quy tại một điểm
Cho hình bình hành \(ABCD\) . Trên các cạnh AB và CD lấy các điểm E và F sao cho AE=CF, trên các cạnh AD và BC lấy điểm M và N sao cho AM=CN.
1)
a) Tứ giác MENF là hình gì ? Vì sao ?
b) Chứng minh các đường thẳng AC,BD,EF và MN đồng quy .
2) Nếu AE = CF = AB : 2 và AM = CN = AD : 2 thì tứ giác MENF là hình gì khi ABCD là hình thoi ? ABCD là hình chữ nhật .
Cho hình bình hành ABCD . Trên các cạnh AB và CD lấy các điểm E và F sao cho AE=CF, trên các cạnh AD và BC lấy điểm M và N sao cho AM=CN.
1)
a) Tứ giác MENF là hình gì ? Vì sao ?
b) Chứng minh các đường thẳng AC,BD,EF và MN đồng quy .
2) Nếu AE = CF = AB : 2 và AM = CN = AD : 2 thì tứ giác MENF là hình gì khi ABCD là hình thoi ? ABCD là hình chữ nhật .
Cho hình bình hành ABCD. Trên tia đối của tia BC lấy điểm E sao cho BE=BC; trên tia đối của tia DC lấy điểm F sao cho CD=DF. Chứng minh rằng:
a) EADB là hình bình hành
b) A,E,F thẳng hàng
c) AC,ED,BF đồng quy
cho hình bình hành ABCD. Trên cạnh AB lấy điểm E, trên cạnh CD lấy điểm F sao cho AE=DF
a) Chứng minh AE//CF, BE//DF
b) chứng minh DE=DF
Cho hình bình hành ABCD. Trên đường chéo AC lấy hai điểm E và F sao cho AE = EF = FC.
a) Tứ giác BEDF là hình gì? Vì sao?
b) Tia DF cắt BC tại M. Chứng minh: DF = 2FM.
c) Tia BE cắt AD tại N, hai đường chéo AC và BD cắt nhau tại O. Chứng minh: M đối xứng với N qua điểm O.