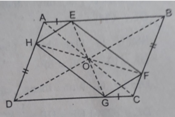
O còn là tâm đối xứng của các hình bình hành: AECG, EBGD, AHCF, DHBF.
Đúng 0
Bình luận (0)
Các câu hỏi tương tự
Cho hình bình hành ABCD. O là giao điểm của hai đường chéo. Trên các cạnh AB, BC, CD, DA ta lần lượt lấy các điểm E, F, G, H sao cho AE = CG, BF = DH. Xác định tâm đối xứng của hình bình hành ABCD.
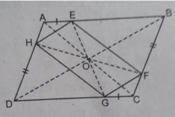
Cho hình bình hành ABCD. O là giao điểm của hai đường chéo. Trên các cạnh AB, BC, CD, DA ta lần lượt lấy các điểm E, F, G, H sao cho AE = CG, BF = DH. Chứng minh EFGH là hình bình hành, tìm tâm đối xứng của nó.
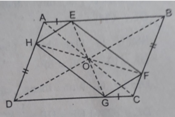
Cho hình bình hành ABCD. O là giao điểm của 2 đg chéo. Trên cac cạnh AB, BC, CD,DA ta lần lượt lấy các điểm E,F,G,H sao cho AE=CG,BF=DH
a, Xác định tâm đối xứng cưa hình bình hành ABCD
b, CM : EFGH là hình bình hành, tìm tâm đối xứng của nó
c, O còn là tâm đối xứng của hình bình hành nào?
Cho hình bình hành ABCD. O là giao điểm của 2 đg chéo.Trên các cạnh AB, BC, CD,DA ta lần lượt lấy các điểm E,F,G,H sao cho AE=CG, BF=DH
a, Xác định tâm đối xứng của hình bình hành ABCD
b, Chứng minh EFGH là hình bình hành, tìm tâm đối xứng của nó
c, O còn là tâm đối xứng của những hình bình hành nào ?
Cho hình bình hành ABCD. Trên các cạnh AB; BC; CD; DA lấy các điểm E; F; G; H sao cho AE = CG; BF = DH. CMR:
a, Xác định tâm đối xứng của hình bình hành ABCD
b, EFGH là hình bình hành và tìm tâm đối xứng
c, Gọi O là giao điểm của AC và BD, O còn là tâm đối xứng của hình bình hành nào?
Cho hình bình hành ABCD . Vẽ ra phía ngoài của hình bình hành các hình vuông có một cạnh là
cạnh của hình bình hành. Gọi E,F,G,H lần lượt là tâm (tức là giao điểm của hai đường chéo) của
các hình vuông vẽ trên các cạnh AB,BC,CD và DA. Chứng minh rằng: EG = HF và EG ⊥ HF.
Cho hình vuông ABCD. Trên các cạnh AB, BC, CD, DA lần lượt lấy các điểm E, F, G, H sao cho AE = BF = CG = DH. Tứ giác EFGH là hình gì? *
Hình bình hành
Hình chữ nhật
Hình vuông
Hình thoi
Cho hình bình hành ABCD tên các cạnh AB, BC, CD, DA lấy tương ứng các điểm E, F, G, H sao cho AE = CG; BF = DH. CMR:
a, EFGH là hình bình hành
b, Các đường thẳng AC; BD; EG; HF cắt nhau tại 1 điểm
Cho tứ giác ABCD. Trên các cạnh AB, BC, CD, DA lấy thứ tự các điểm E,F,G,H sao cho AE=2EB, BF= 1/2FC, CG= 2GD, DH= 1/2HA. CMR : EFGH là hình bình hành