Xét ∆ OED và ∆ OFB, ta có:
∠ (EOD)= ∠ (FOB)(đối đỉnh)
OD = OB (tính chất hình bình hành)
∠ (ODE)= ∠ (OBF)(so le trong)
Do đó: ∆ OED = ∆ OFB (g.c.g)
⇒ OE = OF
Vậy O là trung điểm của EF hay điểm E đối xứng với điểm F qua điểm O
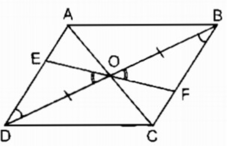
Cho hình bình hành ABCD, O là giao điểm của hai đường chéo. Một đường thẳng đi qua O cắt các cạnh đối AD, BC ở E, F. Chứng minh E và F đối xứng với nhau qua điểm O.
Cho hình bình hành ABCD. Gọi O là giao điểm của hai đường chéo. Một đường thẳng đi qua O cắt các cạnh AD, BC ở E và F. Chứng minh E và F đối xứng với nhau qua O.
Cho hình bình hành ABCD, O là giao điểm của hai đường chéo. Qua O vẽ đường thẳng cắt hai cạnh AB, CD ở E, F. Qua O vẽ đường thẳng cắt hai cạnh AD, BC ở G, H. Chứng minh rằng EGFH là hình bình hành.
Cho hình bình hành ABCD, O là giao điểm của 2 đường chéo. Trên AB lấy E, trên CD lấy F sao cho AE = CF
a) Chứng minh F là điểm đối xứng với E qua O
b) Từ E dựng Ex // AC cắt BC tại I, dựng Fy // AC cắt AD tại K. Chứng minh I và K đối xứng nhau qua O
cho hình bình hành ABCD , O là giao điểm của hai đường chéo. Qua O vẽ đường thẳng cắt hai canh AB , CD ở E ,F . Qua O vẽ đường thẳng cắt hai cạnh AD , BC ở G,H . Chứng minh rằng EGFH là hình bình hành
Cho hình bình hành ABCD, O là giao điểm của hai đường chéo. Một đường thẳng đi qua O cắt các cạnh AB và CD theo thứ tự ở M và N. Chứng minh rằng điểm M đối xứng với điểm N qua O.
Cho hình bình hành ABCD, O là giao điểm của hai đường chéo. Một đường thẳng đi qua O cắt các cạnh AB và CD theo thứ tự ở M và N. Chứng minh rằng điểm M đối xứng với điểm N qua O.
Hướng dẫn:Ta có:ABCD là hình bình hành(gt) =>..............................................
Chứng minh:∆BOM = ∆DON (g.c.g)
Chứng minh: O là trung điểm của MN
=> M đối xứng với N qua O(đpcm)
Cho hình bình hành ABCD, O là giao điểm của hai đường chéo. Một đường thẳng đi qua O cắt các cạnh AB và CD theo thứ tự ở M và N. Chứng minh rằng điểm M đối xứng với điểm N qua O.
Cho hình bình hành ABCD , O là giao điểm của hai đường chéo . Một đường thẳng đi qua O cắt cạnh AB và CD theo thứ tự ở M và N . Chứng minh rằng điểm M đối xứng với điểm N qua O .
