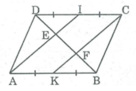
Ta có: AB = CD (tính chất hình bình hành)
AK = 1/2 AB (gt)
CI = 1/2 CD (gt)
Suy ra: AK = CI (1)
Mặt khác: AB // CD (gt)
⇒ AK // CI (2)
Từ (1) và (2) suy ra tứ giác AKCI là hình bình hành (vì có một cặp cạnh đối song song và bằng nhau).
⇒ AI // CK
Trong ∆ ABE, ta có:
K là trung điểm của AB (gt)
AI // CK hay KF // AE nên BF = EF (tính chất đường trung bình tam giác)
Trong ∆ DCF, ta có:
I là trung điểm của DC (gt)
AI // CK hay IE // CF nên DE = EF (tính chất đường trung bình tam giác)
Suy ra: DE = EF = FB
Ta có: AB = CD (tính chất hình bình hành)
AK = 1/2 AB (gt)
CI = 1/2 CD (gt)
Suy ra: AK = CI (1)
Mặt khác: AB // CD (gt)
⇒ AK // CI (2)
Từ (1) và (2) suy ra tứ giác AKCI là hình bình hành (vì có một cặp cạnh đối song song và bằng nhau).
⇒ AI // CK
Trong ∆ ABE, ta có:
K là trung điểm của AB (gt)
AI // CK hay KF // AE nên BF = EF (tính chất đường trung bình tam giác)












