Đáp án B
B = V H ; k ( D ) và H B → = − 2 H D → => k=-2
Đáp án B

B = V H ; k ( D ) và H B → = − 2 H D → => k=-2
Cho hình chữ nhật ABCD tâm I. Gọi E, F, G, H lần lượt là trung điểm của AB, CD, CI, FC. Phép đồng dạng hợp thành bởi phép vị tự tâm C tỉ số k = 2 và phép đối xứng tâm I biến tứ giác IGHF thành:
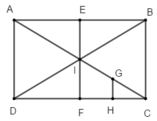
A. AIFD
B. BCFI
C. CIEB
D. DIEA
Cho hình chữ nhật ABCD tâm I. Gọi E, F, G, H lần lượt là trung điểm của AB, CD, CI, FC. Phép đồng dạng hợp thành bởi phép vị tự tâm C tỉ số k=2 và phép đối xứng tâm I biến tứ giác IGHF thành
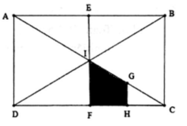
A. AIFD
B. BCFI
C. CIEB
D. DIEA
Cho tam giác ABC. Gọi M , N lần lượt là trung điểm của AB và AC. Phép vị tự tâm A tỉ số k biến M thành B, N thành C. Khi đó k bằng
A. 2
B.-2
C. 1 2
D. − 1 2
Cho tam giác ABC. Gọi M , N lần lượt là trung điểm của AB và AC. Phép vị tự tâm A tỉ số k biến B thành M, C thành N. Khi đó k bằng
A. 2
B.-2
C. 1 2
D. − 1 2
Cho tam giác ABC có trọng tâm G, trực tâm H, tâm đường tròn ngoại tiếp O. gọi D, E, F lần lượt là trung điểm các cạnh BC, CA, AB.
Phép vị tự tâm G tỉ số -1/2 biến A H → thành
A. O D →
B. D O →
C. H K →
D. K H →
Cho tam giác ABC có trọng tâm G, trực tâm H, tâm đường tròn ngoại tiếp O. gọi D, E, F lần lượt là trung điểm các cạnh BC, CA, AB.
Phép vị tự tâm G tỉ số -1/2 biến tam giác ABC thành
A. Tam giác GBC
B. Tam giác DEF
C. Tam giác AEF
D. Tam giác AFE
Cho tam giác ABC có trọng tâm G, trực tâm H, tâm đường tròn ngoại tiếp O. gọi D, E, F lần lượt là trung điểm các cạnh BC, CA, AB. Phép vị tự tâm G tỉ số -1/2 biến:
A. Điểm A thành điểm G
B. Điểm A thành điểm D
C. Điểm D thành điểm A
D. Điểm G thành điểm A
Cho hình chóp S ABCD . có đáy ABCD là hình bình hành tâm O. Gọi M.N.P lần lượt là trung điểm AD,BC và SB a, tìm giao điểm Q của SA và (MNP) b, chứng minh SD//(MNP) và (SMC)//(ANP) c, gọi H=BD ∩ AN, K=BD ∩ MC, i= PK ∩ SH. tính tỉ số SΔSLK/SΔSLP
Cho hình thang ABCD có AB // CD và AB = 2a, BC = CD = DA = a. Đường thẳng d vuông góc với mặt phẳng (ABCD) tại A. Gọi S là một điểm duy nhất thay đổi trên d. (P) là một mặt phẳng qua A vuông góc với SB tại I và cắt SC, SD lần lượt tại J, K.
a) Chứng minh tứ giác BCJI, AIJK là các tứ giác nội tiếp.
b) Gọi O là trung điểm của AB, O' là tâm đường tròn ngoại tiếp tứ giác BCJI. Chứng minh rằng OO' ⊥ (SBC).
c) Chứng minh rằng khi S thay đổi trên d thì JK luôn luôn đi qua một điểm cố định.
d) Tìm một điểm cách đều các điểm A, B, C, D, I, J, K và tìm khoảng cách đó.
e) Gọi M là giao điểm của JK và (ABCD). Chứng minh rằng AM là tiếp tuyến của đường tròn ngoại tiếp tam giác ABC.
f) Khi S thay đổi trên d, các điểm I, J, K lần lượt chạy trên đường nào.