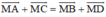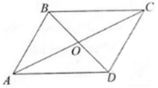
a) Ta có:
O là trung điểm của AC nên 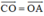
Do đó 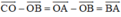
b) ABCD là hình bình hành nên 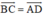
Do đó 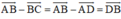
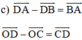
Mà ABCD là hình bình hành nên 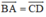
Do đó 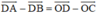
d) ABCD là hình bình hành nên 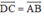
Lại có 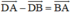
Do đó 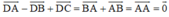

a) Ta có:
O là trung điểm của AC nên 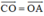
Do đó 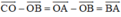
b) ABCD là hình bình hành nên 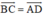
Do đó 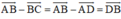
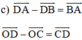
Mà ABCD là hình bình hành nên 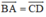
Do đó 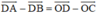
d) ABCD là hình bình hành nên 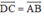
Lại có 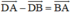
Do đó 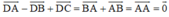
Cho hình bình hành ABCDcó tâm o chứng minh rằng AO-OB
Trong mặt phẳng oxy, cho A(-1;5); B(1;-2); C(3;6) a) Chứng minh rằng A, B, C lập thành một tam giác. b) Tính tọa độ trọng tâm tam giác ABC. c) Tìm tọa độ điểm D của hình bình hành ABCD và tính tọa độ tâm của hình bình hành
1)Cho hình bình hành ABCD, xác định các vectơ DA+DC,AB+DA.
2)Cho 5 điểm A, B, C, D, E. Chứng minh rằng: AC-ED+CD+EC-BC = AB
3)Cho hình vuông ABCD, tâm O cạnh bằng a.
a) Xác định vecto BA+DA+AC, AB+CA+BC, AB+AC.
b) Tính độ dài vecto DA+DC, AB-BC
a) Cho tứ giác ABCD không phải là hình bình hành, AC cắt BD tại O có OB = OD. Gọi M, N lần lượt là trung điểm của AB và CD, MN cắt AC tại I. Chứng minh rằng \(\overrightarrow{MI}=\overrightarrow{IN}\)
b) Cho tứ giác ABCD có 2 đường chéo cắt nhau tại I. Biết \(\overrightarrow{IA}+\overrightarrow{IB}+\overrightarrow{IC}+\overrightarrow{ID}=\overrightarrow{0}\). Chứng minh rằng tứ giác ABCD là hình bình hành
Cho hình bình hành ABCD. Chứng minh rằng: 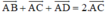
Cho hình bình hành ABCD tâm O. Chứng minh OA+OB+OC+OD= véctơ 0
Cho hình bình hành ABCD có B A D ^ < 90 ∘ . Giả sử O là điểm nằm trong Δ A B D sao cho OC không vuông góc với BD.
Vẽ đường tròn tâm O đi qua C.BD cắt (O) tại hai điểm M, N sao cho B nằm giữa M, D.
Tiếp tuyến tại C của (O) cắt AD, AB lần lượt tại P, Q
2) CM cắt QN tại K, CN cắt PM tại L. Chứng minh rằng K L ⊥ O C .
Cho hình bình hành ABCD có B A D ^ < 90 ∘ . Giả sử O là điểm nằm trong Δ A B D sao cho OC không vuông góc với BD.
Vẽ đường tròn tâm O đi qua C. BD cắt (O) tại hai điểm M, N sao cho B nằm giữa M, D.
Tiếp tuyến tại C của (O) cắt AD, AB lần lượt tại P, Q
1) Chứng minh rằng bốn điểm M, N, P, Q cùng thuộc một đường tròn.
Cho hình bình hành ABCD và điểm M tùy ý. Chứng minh rằng