Các câu hỏi tương tự
Cho hình lập phương ABCD.ABCD có cạnh bằng
2
a
2
Gọi S là tổng diện tích tất cả các mặt của bát diện có các đỉnh là tâm của các mặt của hình lập phương ABCD.ABCD Khi đó
Đọc tiếp
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng 2 a 2 Gọi S là tổng diện tích tất cả các mặt của bát diện có các đỉnh là tâm của các mặt của hình lập phương ABCD.A'B'C'D' Khi đó
![]()
![]()
![]()
![]()
Cho hình đa diện đều loại {4;3} cạnh a. Gọi S là tổng diện tích tất cả các mặt của hình đa diện đó. Mệnh đề nào dưới đây đúng?
A
.
S
6
a
2
B
.
S
4
a
2
C
.
S
8
a
2...
Đọc tiếp
Cho hình đa diện đều loại {4;3} cạnh a. Gọi S là tổng diện tích tất cả các mặt của hình đa diện đó. Mệnh đề nào dưới đây đúng?
A . S = 6 a 2
B . S = 4 a 2
C . S = 8 a 2
D . S = 10 a 2
Cho hình chóp đều S. ABCD có tất cả các cạnh bằng a, điểm M thuộc cạnh SC sao cho SM 2MC. Mặt phẳng (P) chứa AM và song song với BD. Tính diện tích thiết diện của hình chóp S. ABCD cắt bởi (P) A.
3
a
2
5
B.
4
26
a
2...
Đọc tiếp
Cho hình chóp đều S. ABCD có tất cả các cạnh bằng a, điểm M thuộc cạnh SC sao cho SM = 2MC. Mặt phẳng (P) chứa AM và song song với BD. Tính diện tích thiết diện của hình chóp S. ABCD cắt bởi (P)
A. 3 a 2 5
B. 4 26 a 2 15
C. 2 26 a 2 15
D. 2 3 a 2 5
Câu 1. Cho hình chóp S ABC . có SA vuông góc với ABC và đáy ABC đều cạnh a. Biết SA3a/2.Gọi H là trung điểm của BC.a. Tính góc giữa hai mặt phẳng SBC và ABC ?b. Tính diện tích của tam giác ABC từ đó suy ra diện tích tam giác SBC ?c. Chứng minh SBC vuông góc với SAH Câu 2. Cho hình chóp tam giác đều S ABC . có cạnh đáy bằng a và đường cao SH bằng cạnh đáy. Tính số đo góc hợp bởi mặt bên và mặt đáy
Đọc tiếp
Câu 1. Cho hình chóp S ABC . có SA vuông góc với ABC và đáy ABC đều cạnh a. Biết SA=3a/2.Gọi H là trung điểm của BC.
a. Tính góc giữa hai mặt phẳng SBC và ABC ?
b. Tính diện tích của tam giác ABC từ đó suy ra diện tích tam giác SBC ?
c. Chứng minh SBC vuông góc với SAH
Câu 2. Cho hình chóp tam giác đều S ABC . có cạnh đáy bằng a và đường cao SH bằng cạnh đáy. Tính số đo góc hợp bởi mặt bên và mặt đáy
Cho hình chóp tứ giác đều S. ABCD, có cạnh đáy bằng a và có thể tích
a
3
3
6
Gọi J là điểm cách đều tất cả các mặt của hình chóp. Tính khoảng cách d từ J đến mặt phẳng đáy A.
d
a
3
4
B. ...
Đọc tiếp
Cho hình chóp tứ giác đều S. ABCD, có cạnh đáy bằng a và có thể tích a 3 3 6 Gọi J là điểm cách đều tất cả các mặt của hình chóp. Tính khoảng cách d từ J đến mặt phẳng đáy
A. d = a 3 4
B. d = a 3 2
C. d = a 3 6
D. d = a 3 3
Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng 1, góc giữa cạnh bên và mặt đáy bằng 60
o
C
. Gọi A,B,C lần lượt là các điểm đối xứng của A,B,C qua S. Thể tích của khối đa diện ABCABC bằng A.
V
2
3
3
B.
V...
Đọc tiếp
Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng 1, góc giữa cạnh bên và mặt đáy bằng 60 o C . Gọi A',B',C' lần lượt là các điểm đối xứng của A,B,C qua S. Thể tích của khối đa diện ABCA'B'C' bằng
A. V = 2 3 3
B. V = 2 3
C. V = 4 3 3
D. V = 3 2
Cho tứ diện đều ABCD có cạnh bằng a. Gọi E,F lần lượt là các điểm đối xứng của B qua C,D và M là trung điểm của đoạn thẳng AB. Gọi (T) là thiết diện của tứ diện ABCD khi cắt bởi mặt phẳng (MEF). Tính diện tích S của thiết diện (T)
Đọc tiếp
Cho tứ diện đều ABCD có cạnh bằng a. Gọi E,F lần lượt là các điểm đối xứng của B qua C,D và M là trung điểm của đoạn thẳng AB. Gọi (T) là thiết diện của tứ diện ABCD khi cắt bởi mặt phẳng (MEF). Tính diện tích S của thiết diện (T)
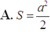


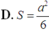
Cho hình chóp S.ABCD có đáy là hình bình hành ABCD, O là giao điểm hai đường chéo, AC a, BD b, tam giác SBD đều. Gọi I là điểm di động trên đoạn AC với AI x (0 0 a). Lấy là mặt phẳng đi qua I và song song với mặt phẳng (SBD).a) Xác định thiết diện của mặt phẳng với hình chóp S.ABCD.b) Tìm diện tích S của thiết diện ở câu a) theo a, b, x. Tìm x để S lớn nhất.
Đọc tiếp
Cho hình chóp S.ABCD có đáy là hình bình hành ABCD, O là giao điểm hai đường chéo, AC = a, BD = b, tam giác SBD đều. Gọi I là điểm di động trên đoạn AC với AI = x (0 < 0 < a). Lấy là mặt phẳng đi qua I và song song với mặt phẳng (SBD).
a) Xác định thiết diện của mặt phẳng với hình chóp S.ABCD.
b) Tìm diện tích S của thiết diện ở câu a) theo a, b, x. Tìm x để S lớn nhất.
Cho hình chóp S.ABC có SA SB SC a,
A
S
B
^
B
S
C
^
C
S
A
^
α
. Gọi là mặt phẳng đi qua A và các trung điểm của SB, SC. Tính diện tích thiết...
Đọc tiếp
Cho hình chóp S.ABC có SA = SB = SC = a, A S B ^ = B S C ^ = C S A ^ = α . Gọi là mặt phẳng đi qua A và các trung điểm của SB, SC. Tính diện tích thiết diện S của hình chóp cắt bởi mặt phẳng ( β )
A . S = a 2 2 7 cos 2 α - 16 cos α + 9
B . S = a 2 2 7 cos 2 α - 6 cos α + 9
C . S = a 2 8 7 cos 2 α - 6 cos α + 9
D . S = a 2 8 7 cos 2 α - 16 cos α + 9





